Gaussの正十七角形

Gaussが正十七角形が描けることを証明したという話は伝説として聞いてはいるが, 高木先生の近世数学史談に詳しく書いてある. 計算を追うのは大変だが, なるほど描けそうだという気分になるには十分である.

角2π/17をφとし, cos φを計算すると

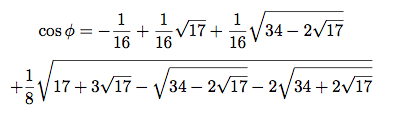
が得られる. 凄い式だが計算機の威力を借りて検算すると,

(+ (/ -1 16)
   (/ (sqrt 17) 16)
   (/ (sqrt (- 34 (* 2 (sqrt 17)))) 16)
   (/ (sqrt (+ 17 (* 3 (sqrt 17)) (- (sqrt (- 34 (* 2 (sqrt 17)))))
      (* -2 (sqrt (+ 34 (* 2 (sqrt 17))))))) 8))
-> .9324722294043558
(define pi (* 4 (atan 1)))
(define phi (/ (* 2 pi) 17))
(cos phi) -> .9324722294043558

と驚く.

cos φが分かればsin φも得られ, 下の左の図のように正十七角形が描ける.

まず単位の長さで線分ABを引く. これが正十七角形の1辺になる. 次にBからcos φだけ右へ延長しCをとり, 上へsin φだけ延長してDをとり, BDを結ぶ. これが次の辺になる. 以下同様に15回繰り返せば, 図のように正十七角形が完成する. もちろんGaussが自分でこういう絵を描いたとは思えない. 私に描けたのは, PostScriptのお蔭である.




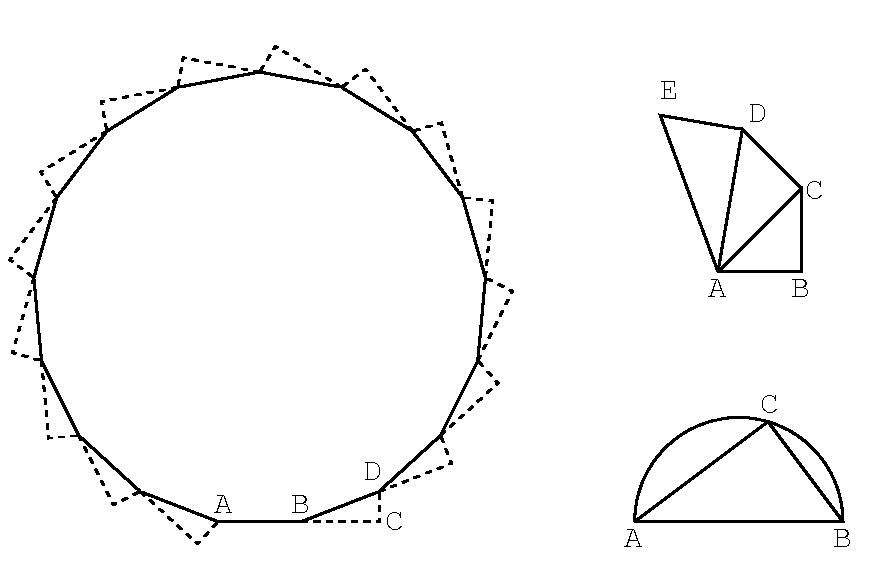
しかし, ルートなんたらが沢山出てくるから, cos φの長さを取るのはおおごとである. 基本的には右上の図のように, AB=1をとり, 直角にBC=1を延すとAC=√2となる. CからACに直角にCD=1を取ると, AD=√3になり, 同様にして整数の平方根はいくらでも取ることが出来る. Gaussの式には√17が沢山現れるが, それには1辺4と1辺1との直角三角形を作れば斜辺は√17になってくれる.

右下の図は√(a-b)の取り方を示す. ABを√aの長さにとり, ABを直径とする半円を描く. BC=√bを円周上にとれば, ACが求めるものである.