再帰曲線

dragon曲線ですぐ思い出すのは, TAOCP(The Art of Computer Programming)4.1にあるtwindragonのフラクタルの絵である.



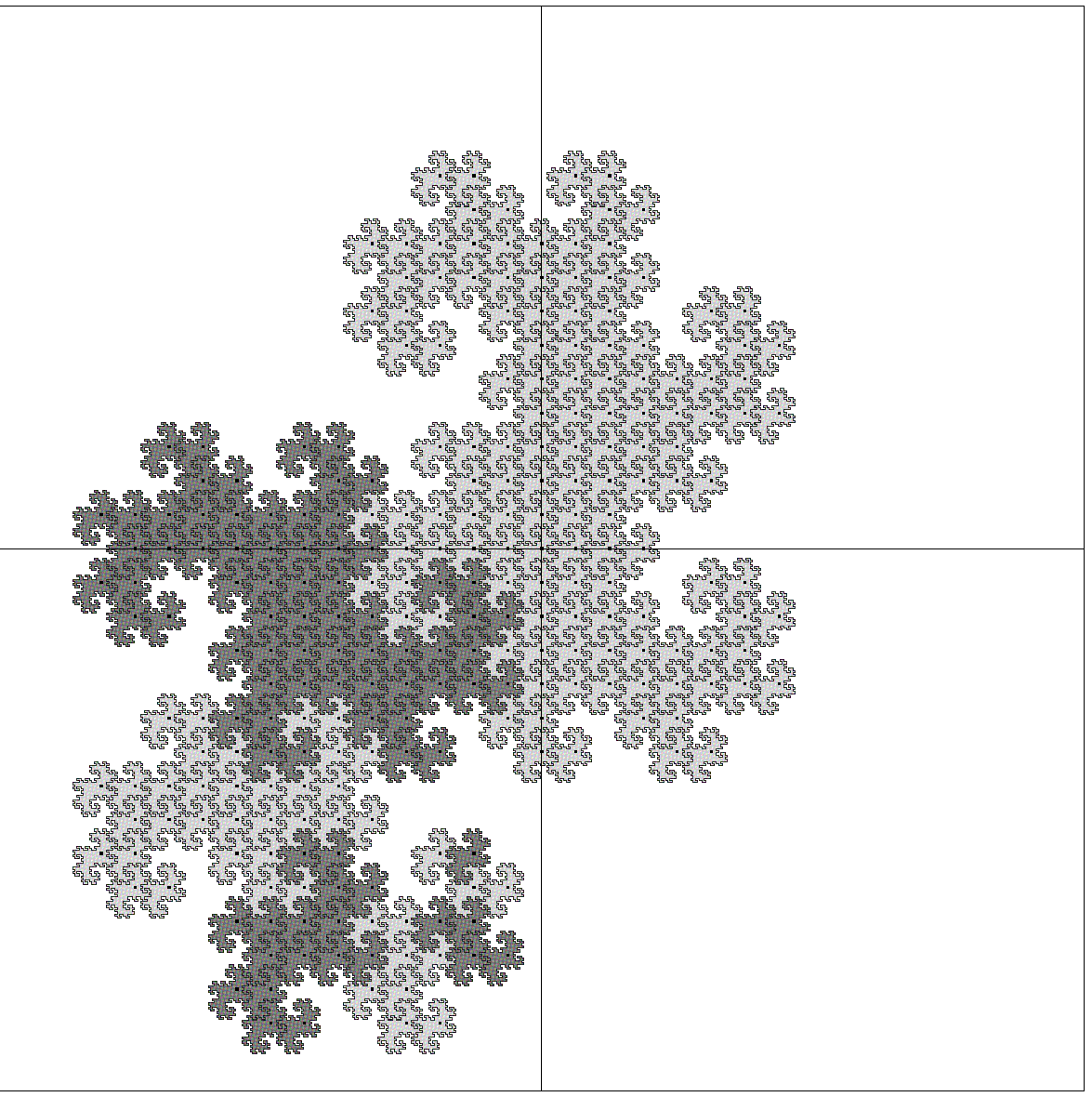
右上に灰色の竜がいる. その左下に黒の半分の大きさの竜がいる. さらにその下に灰色の半分の大きさの竜がいる. この後, 黒, 灰, と交互に小さくなり, 最後は同じ大きさの黒と灰が並んで終る.

よくよく見ると, 一番大きい灰色の竜は, 相似形の小さい竜で出来ている. 小さい竜は128個ある. 黒竜はよく見えないがこれも同様な小竜で出来ている. 最後の竜は, 小竜1個だ.

種明かしをすると, この絵は i-1進法の小数を示すものだ. 通常の2進小数(.a₁a₂a₃a₄...) ₂(a_i=0,1)は,

n = &Sigma _i=1 a_i*2^-i

を表わすが, i-1進法では, この式の2の代りにi-1を使う. iはいうまでもなく虚数単位である.

これらの数の表わす値は,

0.1 =-1/2-1/2i
0.01=+1/2i
0.001=1/4-1/4i
0.0001=-1/4
0.00001=1/8+1/8i
0.000001=-1/8i
0.0000001=-1/16+1/16i
0.00000001=1/16

で, 従って

0    =0
0.00000001=1/16
0.00000010=-1/16+1/16i
0.00000011=+1/16i
0.00000100=-1/8i
0.00000101=1/16-1/8i
0.00000110=-1/16-1/16i
0.00000111=-1/16i

これを複素平面に描くと下のようになる. これは面白いことに, 複素平面を重複せずに覆う.



構造的にはまず中央に0の点が出来る. 0.00000001=1/16なので, この0の点を右へ1単位移動すると1になる. 次に 0.0000001=-1/16+1/16iなので, 0と1の点を左へ1, 上へ1移動すると2と3になる. また0.000001=-1/8iなので, 0,1,2,3を下へ2単位移動して, 4,5,6,7とする. このように, それまで出来た点を次々と移動すればよい. 0.1=-1/2-1/2iなので, 黒い竜は灰色の竜の左下にいたわけだ.

これを256点までとると, 下のようになる.



最初のフラクタルの絵で, 灰色と黒の小竜が並んでいたのは, この図では下から6段目, 一番虚数軸に近い2個である.

Schemeは, 複素数は自家薬籠中の機能なので, こういう計算はなんでもない.

(define mydevice (make-graphics-device 'x))
(define (n2b n m)
 (if (= m 0) '()
     (cons (modulo n 2) (n2b (quotient n 2) (- m 1)))))
(define (evaluate n)
 (if (null? n) 0
   (+ (/ (car n) b) (/ (evaluate (cdr n)) b))))
(define b -1+i)

(do ((i 0 (+ i 1))) ((= i 256))
 (let* ((a (reverse (n2b i 8))) (p (evaluate a))
        (x (real-part p)) (y (imag-part p)))
   (graphics-operation mydevice 'fill-circle x y 0.02)))

(graphics-draw-line mydevice -1 0 1 0)
(graphics-draw-line mydevice 0 -1 0 1)

もうこれはM.C.Escherの世界でもある. 詳しい話はwww.math.uwaterloo.ca/~wgilbert/Research/MathIntel.pdfをご覧あれ.