正三角形を4つのピースに切り分け, 再配置して正方形を作れ. 難問である. この本は同時に解答を示しているが, それでよい理由はそう自明ではない.
まず解答は次の通り. 正三角形ABCの辺ABに中点D, BCに中点Eをとる. AEをEの方向にEBの長さだけ延長しFとする. AFの中点Gを中心に半径GFの円を描き, CBのBの方向への延長上との交点をHとする. Eを中心に半径EHの円を描き, ACとの交点をJとする. AC上にBEに等しくJKをとる. DとKからJEに下ろした垂線の足をそれぞれLとMとする.
正三角形ABCをJE, DL, KMで切り分け, 再配置すると, 同面積の正方形が得られる.
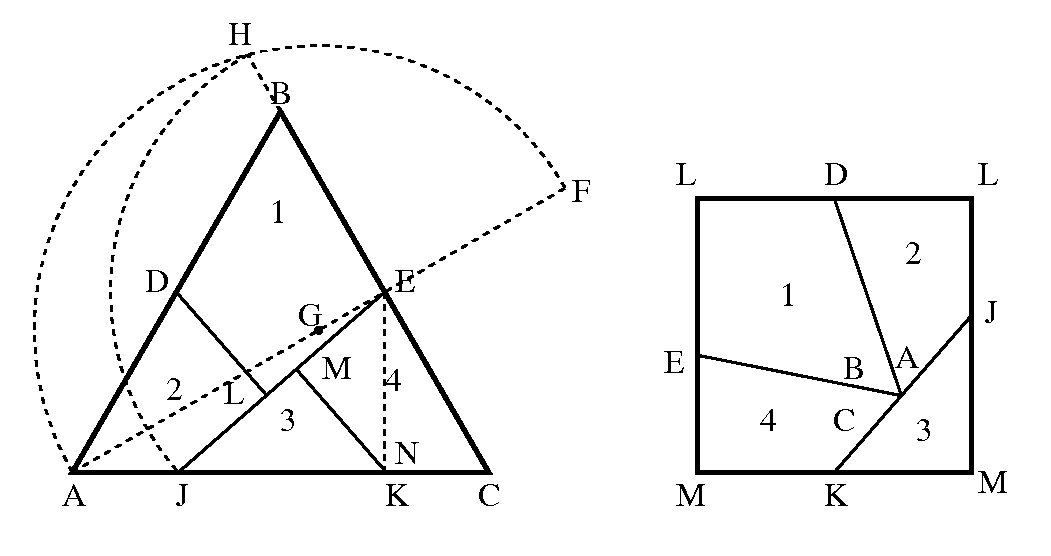
元の正三角形の1辺の長さを2とする. 三角形の高さは√3なので, 正三角形の面積も√3である. 従って同面積の正方形の1辺の長さは√√3である.
上の作り方で出来た正方形の1辺は√√3であろうか.
正三角形の1辺の長さを2とし, 作り方の図で考えると, AE=√3, AF=√3+1, ∴AG=GF=(√3+1)/2, GE=√3-(√3+1)/2=(√3-1)/2. GEHにおいて, EH=√(GH^2-GE^2) =√((√3+1)^2/4)-(√3-1)^2/4)) =√((3+2√3+1)/4-(3-2√3+1)/4)=√√3=EJ. これが作るべき正方形の1辺である.
Eから辺ACに下ろした垂線の足をNとする. EN=(√3)/2. 三角形JENと三角形JKMは相似で斜辺から比は√√3:1. KM=√3/2/√√3=(√√3)/2. つまり正方形の1辺の半分である.
ところで三角形EDLも, DE=JK(=1)だから, JKMと合同である. DL=(√√3)/2.
従って正方形の上と下の辺はLD+LD=MK+MK=√√3.
左の縦の辺は, LE=MJだから, LE+EM=MJ+EM=EJ=√√3. 右の縦の辺も同様. 従って正三角形と同面積の正方形が得られた.
なるほど.
ところで
√√3=1.31607,
A=(0,0), B=(1,√3), C=(2,0), D=(1/2,√3/2), E(3/2,√3/2), JN=√(√3-3/4), AJ=AN-JNなので J=(3/2-JN,0), K=(5/2-JN,0), ∠EJN=atan(EN,JK)=41.15゜
である. NとKはほとんど同じ位置だが, JN=0.99098ゆえ, Kの方がわずかに右にある.

0 件のコメント:
コメントを投稿