再帰曲線

ドラゴン曲線に関する最初のブログ(2009年6月19日)に書いたことだが,...

左折を+, 右折を-と表示すると
+ + - + + - - + + + - - + - -
になる. 記号は15個あるが, 中央の + が最初の折り目で, その両側はもともと重なっていたのを開いたから, 並び順が中央を中心にして対象で, しかも+と-が入れ替わっている.

これを X₂ + Y₂ と書くと,
X₂ = + + - + + - -
Y₂ = + + - - + - -
である. するとこの両枝は同じなので,
X₂ = X₁ + Y₁
Y₂ = X₁ - Y₁
X₁ = + + -
Y₁ = + - -
最後は
X₀ = +
Y₀ = -
この+と-のパターンはなんだろうと思っていたが, はたと思いついたのは, Gray codeであった.

下の図は通常の二進法とGray codeの対応を示す. Gray codeの右の+と-は, Gray codeの1の数が, すぐ上のcodeのそれと較べて, 増えたか減ったかを示す. これが上のパターンと同じなのである.




なぜかというと, 枠で囲った部分がX₂とY₂で, その間が, 一番左の桁が1になったことで + になっているのである.

この図からははみ出すが, 16番のところは右から5ビット目が1になり, +となり, 24番のところは右から4ビット目が0になり, -になるのである.

一方, 通常の二進法の右の小さい丸は, 右から1ビット目と2ビット目, 2ビット目と3ビット目のように, 連続して2つの1が続く状態が現れた場所を示す.

1が連続すると, Gray codeの作り方から分かるように, 排他的論理和をとるので, 1が減るのである.

従って, -が現れるのは, 4n+3か, 8n+6か, 16n+12か, ...である.

これだけ分かるとドラゴン曲線のプログラムは書ける.

(define (test n p)
 (cond ((= (modulo n 4) 3) #f)
       ((= (modulo n 8) 6) #f)
       ((= (modulo n 16) 12) #f)
       ((= (modulo n 32) 24) #f)
       ((= (modulo n 64) 48) #f)
       ((= (modulo n 128) 96) #f)
       ((= (modulo n 256) 192) #f)
       ((= (modulo n 512) 384) #f)
       (else #t)))

山場はこのtestだ. こういつまでも書くわけにはいかないから, nがどんなに大きくてもいいように, 下のプログラムでは書き直してある.

(define (moveto x y)
 (display (number->string x)) (display " ")
 (display (number->string y)) (display " moveto\n"))

(define (rlineto x y)
 (display (number->string x)) (display " ")
 (display (number->string y)) (display " rlineto\n"))

(define limit 64)

(define (test n p)
 (cond ((> p (* 2 n)) #t)
       ((= (modulo n p) (* 3 (/ p 4))) #f)
       (else (test n (* p 2)))))

(define (foo n dx dy)
 (rlineto dx dy)
 (if (< n limit)
  (if (test n 4) (foo (+ n 1) (- dy) dx)
                 (foo (+ n 1) dy (- dx)))))
(moveto 0 0)
(foo 1 20 0)

再帰曲線

このブログにドラゴン曲線のことを書いたのは, 1年くらい前のことである.

ウェブでドラゴン曲線の画像を眺めていたら, 4つのドラゴン曲線を組合わせて, 平面を埋めている絵があった. 早速描いてみることにした. 次がその戦果である.


もちろんドラゴン曲線は角で直角に曲がるのだが, 通過の仕方が分かるように, 四角の部屋を丸く掃く居候モードで描いてある.

問題は, それぞれの色のドラゴンが重ならないかということだ.

ちゃんと証明するのは面倒だが, ドラゴン曲線をフラクタルで描くステップを考えると, 当たり前のような気がする.

フラクタルでの描き方は次のようだ.



まず0次の線を赤のように引く. 左から右に向って引いている積りだ.
次に1次の線を青のように, 赤の線分を右に三角形に膨らませるように引く.
2次の線は, 橙のように, 青の線分を最初は右に, 次は左に膨らませる.
3次の線は, 緑のように, 橙の線分を右, 左, 右, 左と膨らませる.
これを適当な次数まで繰り返す.

描画アルゴリズムとしては, n次のフラクタルを描きたいというサブルーチンで始める. 次数が0なら始点と終点を引く. そうでないなら, n-1のフラクタルのサブルーチンを呼ぶのである.


このようにして描いた, 0次, 2次, 4次, 6次は次のとおりである. 8次の図はこのブログ先頭のものだ.






重ならない理由がなんとなく納得出来たであろうか.

ついでに10次と12次の図も示すと次のとおり.

ビットの反転と置換

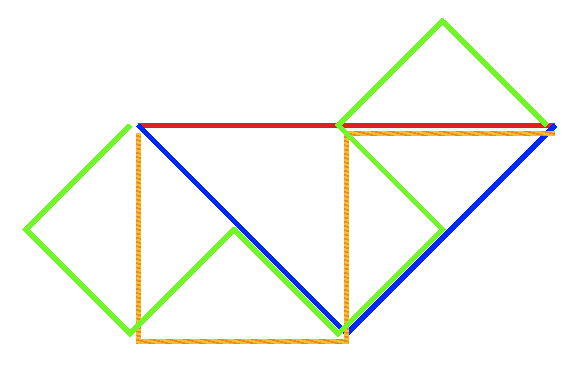
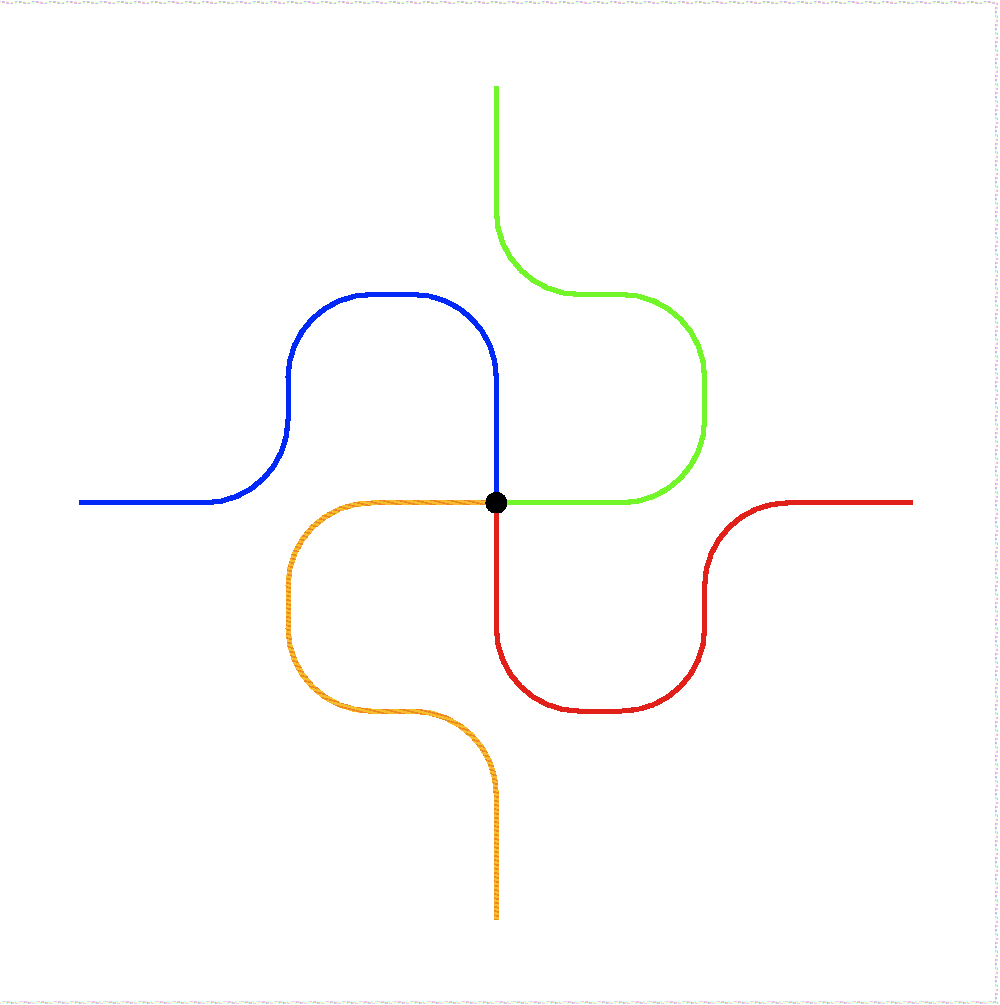
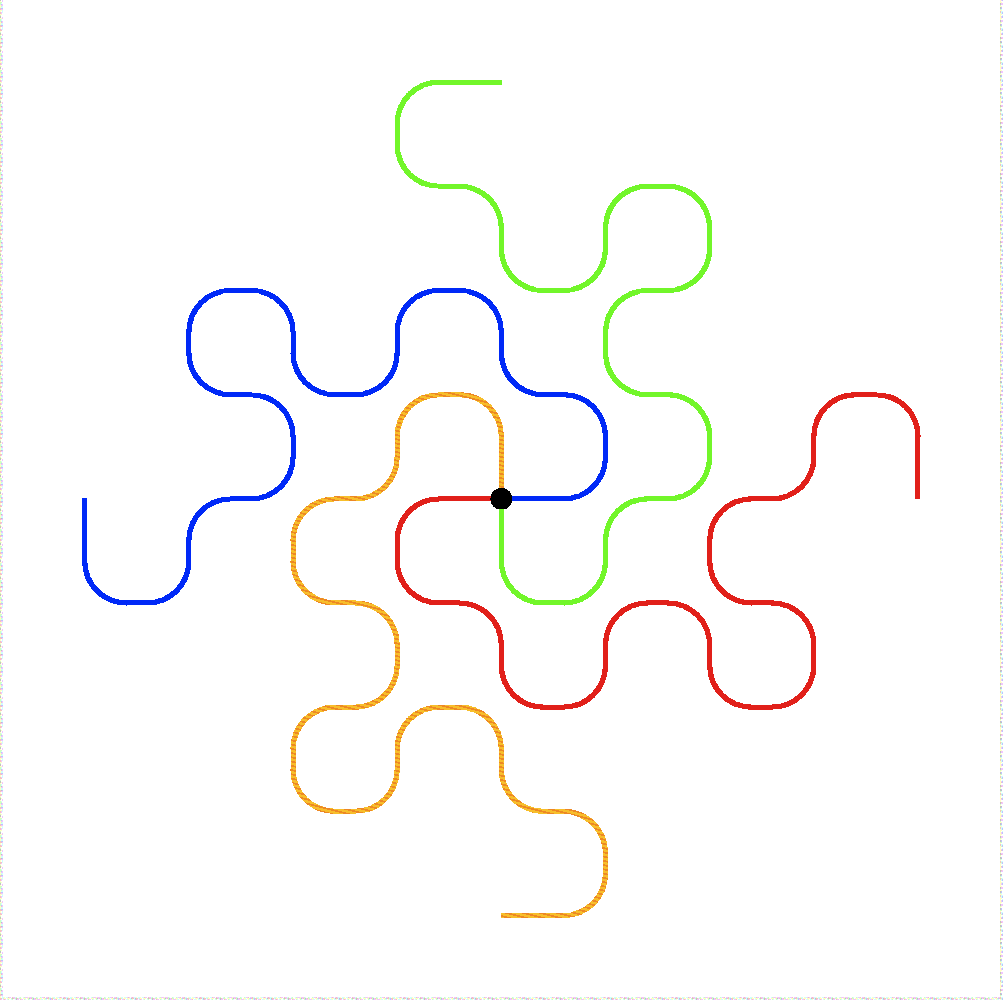
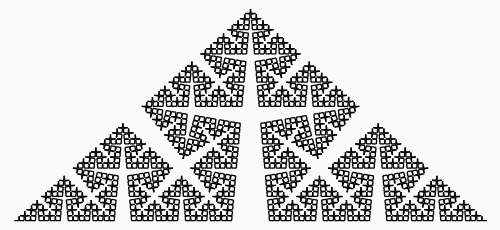
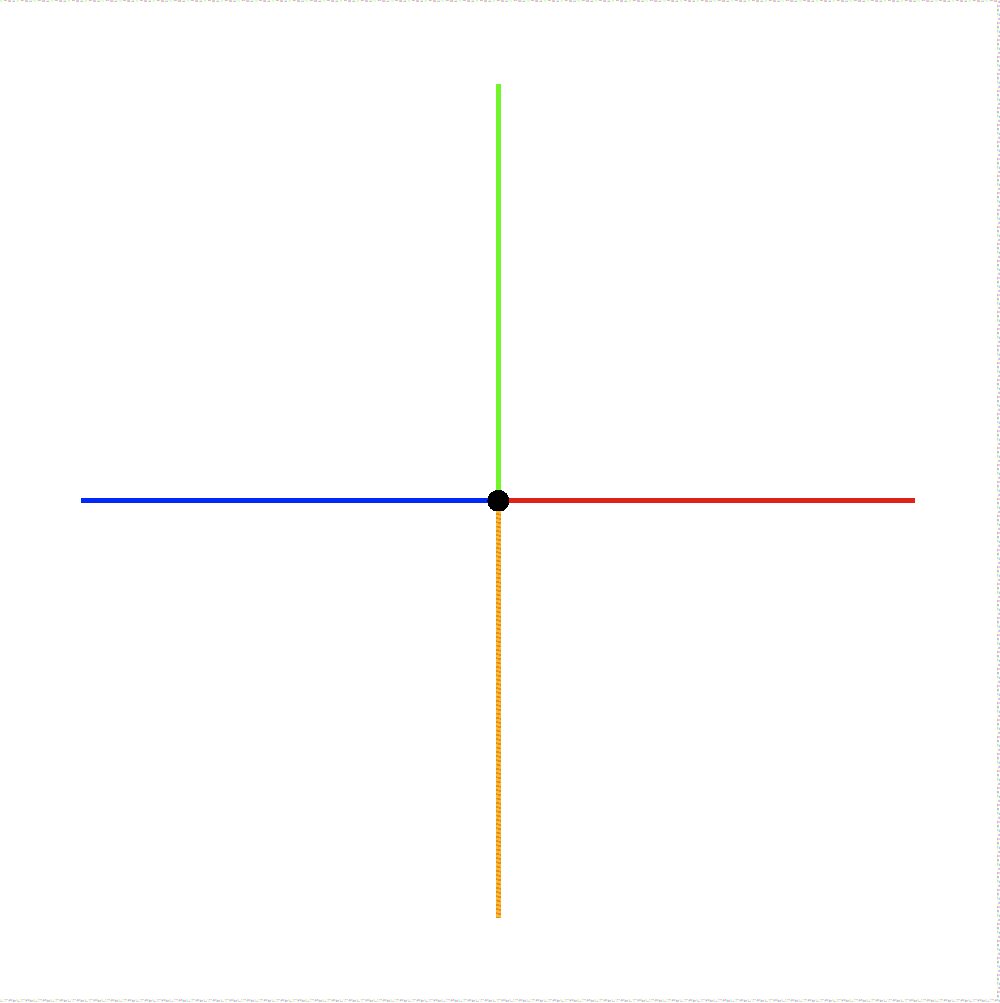Hacker's DelightにもTAOCPにもSchroeppelのビット反転法の話が登場する. もとはHAKMEMの167項の一部にある話である.

Hacker's Delightでは(102ページ), 64ビットレジスタで7ビットxの反転を((x*0x40100401)&0x442211008)%255 と書いてあり, TAOCP(V4F1,26ページ),0<=x<2^gの反転をt←((ax mod 2ⁿ)&b, y←((ct)mod 2ⁿ)>>(n-g) ただしn=g², 0≤x<2^g, a=(2^n+g-1)/(2^g+1-1), b=2^g-1(2ⁿ-1)/(2^g-1), c=(2^n-g-1)/(2^g-1-1) とある.

まずDelightの方.

((x*A)&B)%255
ただし A=0x40100401, B=0x442211008 と書き直す.

このAとBを二進にする.
A=100 0000 0001 0000 0000 0100 0000 0001
つまり4つの1の間に0が9個ある.
B=100 0100 0010 0010 0001 0001 0000 0000 1000

従って 7ビットgfedcbaにAを掛けると

                              gfedcba
      1000000000100000000010000000001  A
gfedcba000gfedcba000gfedcba000gfedcba  A*x
  10001000010001000010001000000001000  Bでマスクすると
  e   a    f   b    g   c        d     これらが残る
43210 6543210 6543210 6543210 6543210  8ビット内の位置
                             11111111  28-1で割った剰余
                              abcdefg  反転出来た.

ビットに右から番号をつけるとaの位置は0, bは1, ..., gは6.
Aを掛けるとaの位置は0,10,20,30になり, 8の剰余は0,2,4,6になる. Bで6のaを取る. bの位置の8の剰余は1,3,5,7で5のものを取る. そういう仕掛けである.

TAOCPの方は, 定数に(2^p-1)/(2^q-1)が多いが, これはqビットごとの1のあるパターンを作る常套手段である.

g=3とすると, n=9. 従って

a=100010001
b=100100100
c=10101

x=rqp
これにa=100010001を掛けると
rqp0rqp0rqp
2nでmodをとると
  p0rqp0rqp
b=100100100
でマスクする
  p00q00r00
c=10101を掛けると
    p00q00r00
  p00q00r00
p00q00r00
p0pqpqrqr0r00
2nでmodをとると
    pqrqr0r00
n-gビット右シフトすると
          pqr
と反転出来る.

これは, 反転すべきパターンを位相をずらして複製し, 必要な部分を取り出し, Delightのように2ⁿ-1で割った剰余で揃えるか, TAOCPのように(割り算は出来ない)cをかけて混ぜ合わせ, 途中に出来た部分を取り出すかである.


TAOCPのやり方で, もっと一般的な置換が出来ないか考えたのが, 今回のブログのテーマである. 例として64ビットレジスタで8ビットのパターンを任意に置換する.

x=76543210 (ビットの名前)
とする.
置換は (0,1,2,3,4,5,6,7)->(3,2,4,1,6,0,5,7)
つまり75061423にしたい.

次のようにする.
a=0x8040201008040201
b=0xbfdfeff7fbfdfeff
y=(xa % 2^64) & b
c=0x0101010101010101
d=0x4020100804020100
z= ((xc % 2^64) >> 1) & d
m=0x14012000000a4080
(((y|z & m) * c) & (2^64-1)) >> 56

Schemeでは
(define (genperm x m)   ;m permutation mask
 (let* ((a #x8040201008040201) (b #xbfdfeff7fbfdfeff)
        (c #x0101010101010101) (d #x4020100804020100)
        (y (band (modulo (* x a) (expt 2 64)) b))
        (z (band (>> (* x c) 1) d)))
  (>> (band (* (band (bor y z) m) c) (- (expt 2 64) 1)) 56)))
(define m #x14012000000a4080)
実行してみると
(genperm #b11110000 m) => #b11010100
(genperm #b11001100 m) => #b10010011
(genperm #b10101010 m) => #b11001001

yはこうなる.

y=      mask
76543210 ff 64ビットの内 最右の8ビット
6543210x fe
543210x7 fd
43210x76 fb
3210x765 f7
210x7654 ef
10x76543 df
0x765432 bf 最左の8ビット x: ドントケアビット

xc>>1 はこうなる.

07654321
07654321
07654321
07654321
07654321
07654321
07654321
?7654321   ?: 右シフトで左から挿入されたビット

z= ((xc mod 2^64) >>1) & d

z=      mask
xxxxxxxx 00
xxxxxxx1 01
xxxxxx2x 02
xxxxx3xx 04
xxxx4xxx 08
xxx5xxxx 10
xx6xxxxx 20
x7xxxxxx 40

y|z は各列に0から7を1つずつ含む.

y|z & 0x14012000000a4080 <= 置換用マスク

76543210 7        80
65432101  5       40
54321027     1 2  0a
43210376          00
32104765          00
21057654   0      20
10676543        3 01
07765432    6 4   14
         75061423

0x0101010101010101を掛ける.

          7
          75
          75  1 2
          75  1 2
          75  1 2
          750 1 2
          75061 23
          75061423

modulo 2^64 >> 56 => 75061423

完成!

置換用マスクの作り方.

00 09 18 27 36 45 54 63
08 01 10 19 28 37 46 55
56 17 02 11 20 29 38 47
48 57 26 03 12 21 30 39
40 49 58 35 04 13 22 31
32 41 50 59 44 05 14 23
24 33 42 51 60 53 06 15
16 25 34 43 52 61 62 07

y|zの行列を眺めながら作った上の表は, 0を0へ移動するには0にマスクを置く. 0を1へ移動するには9にマスクを置く. ... 0を7へ移動するには63にマスクを置く. ...7を7へ移動するには7にマスクを置く. のように読む

この表は pをqに移動するマスク位置を計算するプログラムでも計算出来る.

(define (pq p q)
(cond ((< p (+ q 1)) (+ (* -8 p) (* 9 q)))
      ((= p (+ q 1)) (+ (* 8 p) q))
      ((> p (+ q 1))  (+ 72 (* -8 p) (* 9 q)))))

上の例 0->5 1->3 2->1 3->0 4->2 5->6 6->4 7->7

(number->string
 (apply +                              
(map (lambda (p q) (expt 2 (pq p q)))
  ;from pos          to pos
 '(0 1 2 3 4 5 6 7) '(5 3 1 0 2 6 4 7))
) 16)
=> "14012000000A4080"

再帰曲線

第1回のArtificial LifeのProceedings(1987年)を見ていたら, 下のようなフラクタルの絵があった.



当然どう描くのか不思議であるが, Wikipediaに85度というヒントがあったので, 描いてみたら, 何とも簡単であった.



をまず描くのである. この4本の線をまたフラクタルにすると,





と細かくなり, 何段目かで最初の図になる.



原点からx軸に沿い, 長さdの線を描くとする. その線を途中で折曲げて上のように描きたいから, まずd1を計算する. d1=d/(2+2*cos 85)なのは容易に分かる. 従ってdの線を描く代りに, x軸に沿い, 長さd1の線を描き, 原点を(d1,0)へ移し, そこで85度回転する. また新しいx軸に沿い,長さd1の線を描き, 原点を(d1,0)へ移し, 今度は-170度回転する. 後は図に従い, 同様にやる.

長さdの線を描く代りに, 短い線を何本か描くので, 再帰呼出しになっている. 当然どこかで止めなければならない. nなるパラメータを1つ用意し, 下請けを呼ぶ時, nを1引く. nが0で呼ばれたら, dの直線を直接引く.

PostScriptのプログラムは以下の通り.

/draw {4 dict begin
/n exch def /d exch def %パラメータを取り込む
n 0 gt                  % n>0なら
{/d1 d 85 cos 1 add 2 mul div def /n1 n 1 sub def
gsave                   %環境を待避
d1 n1 draw
d1 0 translate
85 rotate
d1 n1 draw
d1 0 translate
-170 rotate
d1 n1 draw
d1 0 translate
85 rotate
d1 n1 draw
grestore}               %環境を回復
{0 0 moveto d 0 lineto stroke} ifelse end} def % n=0なら直接描く

40 40 translate
400 6 draw              %起動

最終の姿は, 予想もしないものだ.