板チョコ分割

数日前に書いた私のツィッター

割れ目でm×nのピースになる板チョコ. 割れ目に沿って割りピースにまで分ける時の割る回数は, 割る順に関係なく一定とパズル本にあった. 証明は易しい. トーナメントの試合数を思い出す.

について書いてみたい.

これは先頃頂いた, ピーター・ウィンクラー著, 坂井, 岩沢, 小副川訳「とっておきの数学パズル」にあったものだ. 8.11

やってみよう.



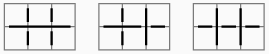
2×3だと, たしかにすべて5回だ.



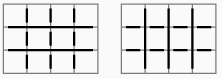
3×4だと, 11回. ということは, m×n-1かもしれない.

そこで数学的帰納法のお出ましとなる.



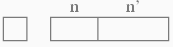
m×nに分割する回数をf(m,n)と書き, m×n-1であろうとして証明する. f(1,1)は分割するまでもなく1区画になっているから, 1×1-1=0だ.

n≥1,n'≥1,n+n'>1について, nとn'の幅に分割したとする. 分割に1回かかるから, f(1,n+n')=f(1,n)+f(1,n')+1={仮定により}(n-1)+(n'-1)+1=n+n'-1. 横1列の板チョコの分割はf(1,n)=n-1で良さそうである.




今度は縦がm≥1,m'≥1でm+m'列ある板チョコを, m列とm'列に分割したとする. 分割に今度も1回かかるから,

f(m+m',n)=f(m,n)+f(m',n)+1={仮定により}(m×n-1)+(m'×n-1)+1
=(m+m')×n-1

確かにf(m,n)=m×n-1であった.


こんなに簡単な式だと, もっと別のエレガントな考え方がありそうだ.




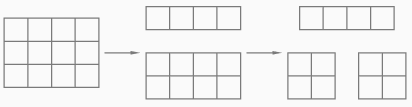
板チョコは最初 ひと(1)塊である. 1回分割すると, ふた(2)塊になる. そのいずれかを分割すると, 3塊になる. つまり, t回分割すると, t+1塊が得られる. 斯くしてm×n塊が得られるまでには, m×n-1回の分割が必要なのであった.


問題を解くとき, とりあえず絶対に答がえられそうな, 正面からの道をとる. それで答が得られてから, 次にもっとうまい手がないか探すのが, 私の普段のやり方だ. プログラムを書くときもそうで, きたなくてもよいから, まず動くプログラムを書く. すると見通しがよくなり, さらにきれいで速いプログラムが得られるのである.