英国ケンブリッジ大学の
EDSAC(Electronic Delay Storage Automatic Calculator)が稼働し始めたのは1949年5月6日であった.
EDSACのメンバーはプログラムの解説書(Maurice V. Wilkes, David J. Wheeler, Stanley Gill: The Preparation of Programs for an Electronic Digital Computer)を早々に出版した. 世界で最初のプログラムの本であり, 多くの人がそれでプログラミングの楽しさを知った. 私もその1人である.
遠い昔のテクニックはどんどん忘れ去られる. 最近EDSACのプログラムを眺める機会があったので, その頃のプログラムを解説したくなった.
当時のメモリーは水銀遅延線かブラウン管であった. EDSACはそのDelay Storageから分かるように, 水銀遅延線の記憶装置を持つ. つまり水銀タンクの一方からPiezo効果を使い音波を送り, 反対側で受けた音波を逆Piezo効果で電
気信号にもどす. その遅れを記憶装置として利用する. (水銀遅延線の写真は
ここに)
EDSACのアーキテクチャは簡単である. レジスタとしては71ビットのアキュムレータと35ビットの乗算レジスタ. 記憶装置は17ビットの短語が1024語. 2n番地と2n+1番地の短語を2語つなぐと35ビットの長語になる. 不思議な計算だがその秘密は, 水銀遅延線での短語は18ビット分あり, 語と語の切替えに1ビットの時間がかかるので, 長語は36-1ビット, 短語は18-1ビット, アキュムレータは72-1ビットということだ.
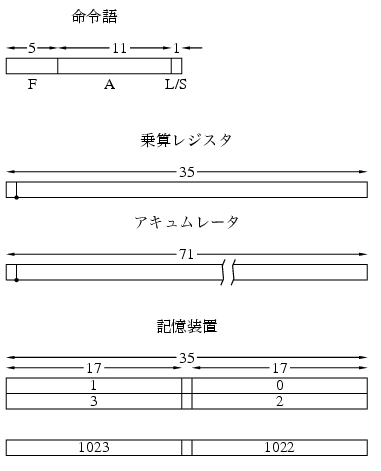
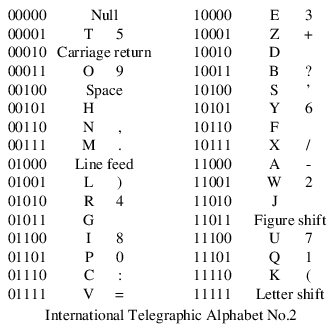
命令語は左端の5ビットが英文字1字で表すファンクション部, 次の11ビットがアドレス部, 最後の1ビットがL/S(long or short)部で, 0だとアドレス部の短語, 1だと長語を示す.
数値は2の補数表示で, -1≤x<1の範囲の値を持つ. 左端のビットが1なら負数である. 具体的には左端の方だけを示すと, 0.01
2は0.25, 0.1
2は0.5, 0.11
2は0.75, 1.00
2は-1,
1.1
2は-0.5, 1.01
2は-0.75である.
EDSACの命令は A n F のように書く. 先頭の英字がファンクションで, つづいて十進でアドレスを書き(0なら何も書かない), 最後のコードレターという英字を書く. コードレターはアドレスの終りを示す他, FはL/Sビットが0, Dは1を示す.
A n はn番地の内容をアキュムレータに足す; S n は引く. T n はアキュムレータをn番地に格納してアキュムレータをクリア. U n は格納するがクリアせず. E n Fはアキュムレータが正ならn 番地へジャンプ, G n F は負ならジャンプで, 無条件ジャンプはなかった.
乗算は乗数を H 命令で乗算レジスタに置き, V n はn番地と乗算レジスタを掛けて積をアキュムレータに足す; N n は積を引く.
EDSACに除算命令はない.
基本的な説明は以上で終る. サブルーチンジャンプの説明も要ろう. n番地からm番地にあるサブルーチンを呼ぶには, 引数を指定された場所に入れ(T 命令で入れるからアキュムレータはクリアされている)n番地に A n F の命令を置く. n+1番地に E m F を置く. 英文字Aは左端のビットが1なので, アキュムレータは負, 従って E 命令でm番地へジャンプする.
m番地のサブルーチンに来たときは, アキュムレータに A n F があるから, これに U 2 F を足す. EDSACの文字コードでは A+U=E だから和は E n+2 F の命令になり, これをサブルーチンの最後に格納する. サブルーチンからはこの命令を実行してn+2番地へ戻る. これをWheelerリンケージという.
次は二進法の小数を十進に変換して出力する方法.
0.0001
2は十進では0.0625である. これを10倍する. 二進の方は0.1010
2, 十進の方は0.625 この時の整数部が元の小数の1桁目だが, 今は0だから0を出力.
また10倍する. 二進は110.0100
2, 十進は6.25. 整数部は6だから6を出力. 整数部を捨ててまた10倍する. 二進は10.1
2, 十進は2.5. そこで2を出力. さらに10倍して5を出力. という次第で0625が出来る.
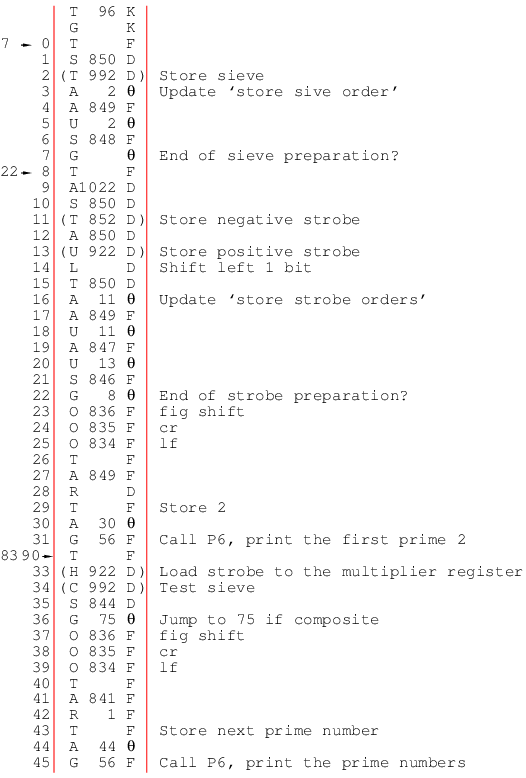
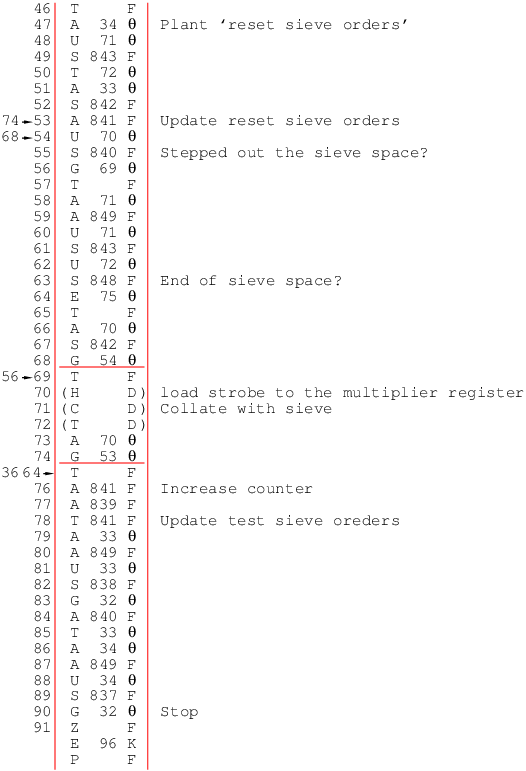
EDSACのプリントルーチンP6は次のように書いてある.

左の0から31は相対行番号である. 欄外の24→9のようなのは, 24番地から9番地へジャンプして來るの意味. 25行目の(E F)のかっこは, この命令は変更されること. その下の横線は, 無条件ジャンプを示す. 29番地から31番地の左の2本の縦線は, 偽命令, つまり命令の形はしているが実行されず, 定数であることを示す.
最初の G K はKで終っているから, 制御指令で, 次の命令が格納される番地を相対番地の原点に設定する. つまり命令がθ(短語)やπ(長語)で終っている時は, A 3 F 命令の場所を0 とする. 以下では相対番地を'で示す.
0',1'番地はWheelerリンケージである. 帰り命令は25'番地に格納される. 2'番地は29'番地の偽命令を乗算レジスタに置く. Jは01010, 995は二進では1111100011
2で, 最後がFつまり0だから, 命令の形としては
01010 01111100011 0
であり, 数値的には
(/ #b01010011111000110 65536.0) => .655364990234375
だから, 2
16/10
5を上に丸めたものである.
0番地には短語の範囲に5桁の整数があり, それを5桁で出力するのだが, 最大の99999と最小の1とを見ると,
1 ]=> (* (/ 99999 65536) .655364990234375)
;Value: .9999976144172251
1 ]=> (* (/ 1 65536) .655364990234375)
;Value: 1.00000761449337e-5
だから, 純小数にして5桁出力する方針である.
4'番地の T 4 D でこうして出来た長語を4,5番地に置く. 5',6'番地は3'番地の命令V F を0番地に入れる. Vは11111なので, コメントのように-1/16を置くことになる. 0番地の負は, 出力の先頭の0をスペースにする目印である.
7'番地は乗算レジスタに10/16を置き, 10倍の準備をする.
8'番地は6'番地の命令を0から引き, Tが00101, 5なので1番地のカウンタを-5/16にする. 10'番地は4,5の長語に10/16を掛ける, すなわち10倍して小数点を4ビット右へ. つまり整数部が先頭の5ビットに収まる.
11'番地ではアキュムレータを残したまま積を戻し, 12'番地の A F で6'番地で入れた0番地の-1/16を足す, つまり整数部が0だったら-1/16になり, 26'番地へ進む. 26'番地で先程引いた1/16を足し, O 31 θ で空白を出力, 20'へ戻る.
整数部が0でなければ, 13'番地のジャンプは起きず, 14'番地の T F でアキュムレータをクリアし, 15'番地の T F で0番地を0にする.
16'番地の O 5 F は, 4番地の長語の先頭の5ビットが数字のコードなので, それを出力する.
17'番地で4番地の長語を取り出し, F 4 F では O 5 F で出力レジスタにいれた数字のコードを4番地の先頭の5ビットに取り出す. 残りのビットは0. それを19'番地で引き, 整数部をなくしてから, L 4 F で左へ4ビットシフト, 4番地へ戻す.
EDSACのシフトは難しい. 命令の下位から見て最初の1のビットが現れるまでシフトする. だから L D は1ビット, L 1 F は2ビット, L 2 F は3ビット, L 4 F は4ビットシフトになる. それより上に1のビットがあっても影響しない.
22'番地からは5桁出力したかのチェック. 最初に入れた1番地の-5/16から3'番地の-1/16を引く. 初めの4回は負なので9'番地へ戻る. 5回済むと25'から主ルーチンに戻る.
思わず長い説明になったが, EDSACの頃のプログラムはこういう感じであった.
このプログラムの問題点は0を出力すると, 5個の空白になることだ. 当時はメモリーが少く, プログラムを短かくするのが重要であった.
EDSACについては,
シミュレータのTutorial Guideを参照されたし. その23ページにP6の記述がある.


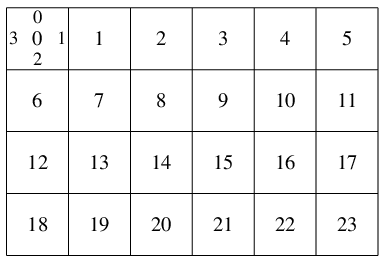

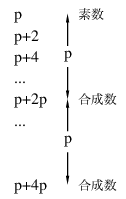 篩は正のストロブを順に使い, 篩の右から順のビットとandをとって, 素数か合成数かをみる. 合成数なら次のストロブで次の篩のビットを調べに進む. 素数ならその素数をp とすると, 左の図のようにpビットごとにpの倍数があるから, 負のストロブを使っていま調べたビットからpビットおきに篩のビットを0に変えていく. 手順としてはこれだけだが, ストロブが下まで来たときに, 篩を次の長語にする; ストロブを先頭に戻す作業が必要である.
篩は正のストロブを順に使い, 篩の右から順のビットとandをとって, 素数か合成数かをみる. 合成数なら次のストロブで次の篩のビットを調べに進む. 素数ならその素数をp とすると, 左の図のようにpビットごとにpの倍数があるから, 負のストロブを使っていま調べたビットからpビットおきに篩のビットを0に変えていく. 手順としてはこれだけだが, ストロブが下まで来たときに, 篩を次の長語にする; ストロブを先頭に戻す作業が必要である. 



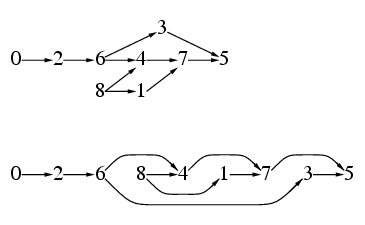 この関係をグラフにすると, 上の図の上のようになる.
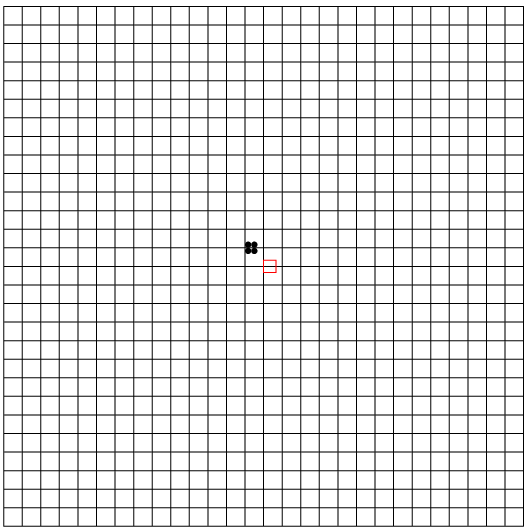
この関係をグラフにすると, 上の図の上のようになる. 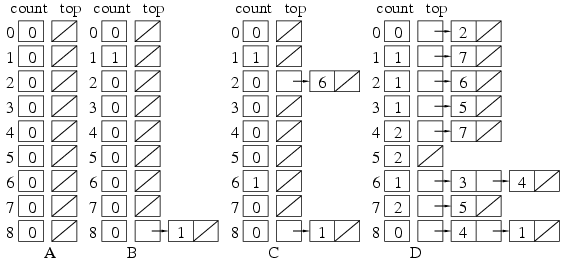 8<1を読み込むと, 要素1には先行者8があったので, 1のcountを1増やし, 1を要素8のtopのリストにつなげる. したがってデータ構造はBのようになる.
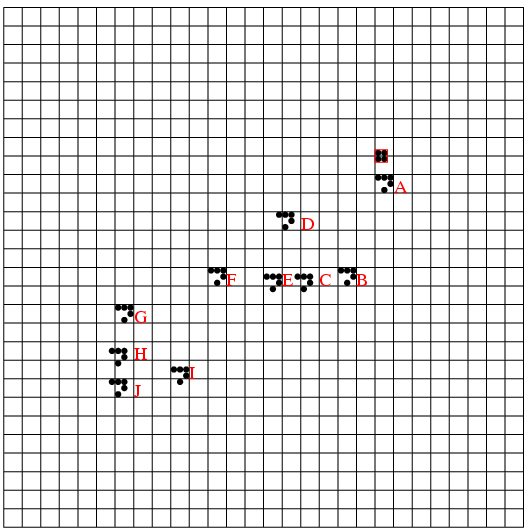
8<1を読み込むと, 要素1には先行者8があったので, 1のcountを1増やし, 1を要素8のtopのリストにつなげる. したがってデータ構造はBのようになる.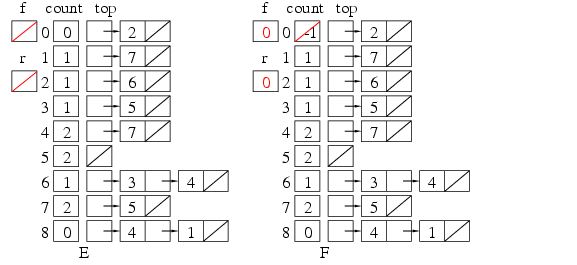 キューを作るには, 先頭(Front)から末尾(Rear)へ至るリストを使う. キューの最後にはnilを入れておく. キューに要素を挿入するのは末尾の側で, 削除するのは先頭の側である. その場所を覚えるためにの変数fとrを用意し, キューが空の時は, f=r=nilとする(E).
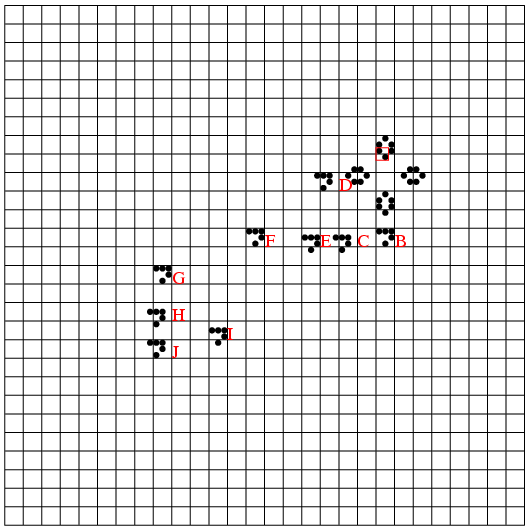
キューを作るには, 先頭(Front)から末尾(Rear)へ至るリストを使う. キューの最後にはnilを入れておく. キューに要素を挿入するのは末尾の側で, 削除するのは先頭の側である. その場所を覚えるためにの変数fとrを用意し, キューが空の時は, f=r=nilとする(E). 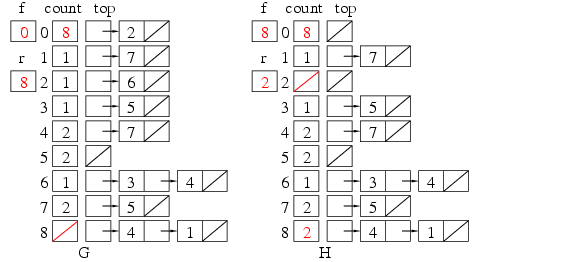 まずfの値0を出力, N=N-1とする. 0のtopからリストを辿り, それらに先行していたものがなくなった処理をする. つまり要素2のcountを1減らす. その結果countが0になったら, この要素も先行するものがなくなり, 出力できるようになったわけで, この要素をcountのキューにつなぐ(H). 0のcountは8のままだが, これはゴミである. Algorithm 2.2.3-Tでは, topのリストはそのままにしているが, 演習問題2.2.3-23にあるように, トポロジカルソートが出来なかったときの原因探索用に, 済んだリストはnilにしておくのがよい.
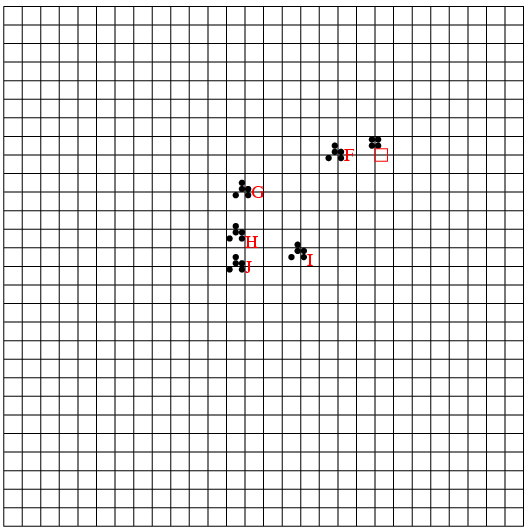
まずfの値0を出力, N=N-1とする. 0のtopからリストを辿り, それらに先行していたものがなくなった処理をする. つまり要素2のcountを1減らす. その結果countが0になったら, この要素も先行するものがなくなり, 出力できるようになったわけで, この要素をcountのキューにつなぐ(H). 0のcountは8のままだが, これはゴミである. Algorithm 2.2.3-Tでは, topのリストはそのままにしているが, 演習問題2.2.3-23にあるように, トポロジカルソートが出来なかったときの原因探索用に, 済んだリストはnilにしておくのがよい.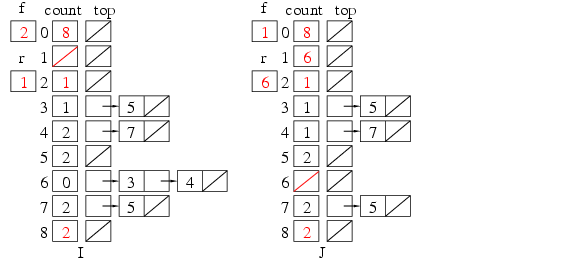 図Iは要素8も出力したところ, Jは2も出力したところである. キューの先頭をfで辿り出力を続ける. fがnilになったら終わりで, Nは0になったはずである. 0にならなければ, 元のデータがおかしかった(ループがあった)ので, topのリストを出力してみると, 原因がわかる.
図Iは要素8も出力したところ, Jは2も出力したところである. キューの先頭をfで辿り出力を続ける. fがnilになったら終わりで, Nは0になったはずである. 0にならなければ, 元のデータがおかしかった(ループがあった)ので, topのリストを出力してみると, 原因がわかる.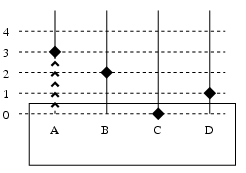 A, B, C, などが記憶場所で, その上方にブロックを置き, そのブロックまでの距離を記憶している値とする. 従って書き込むにはその数値の分だけブロックを遠ざける手続きを繰り返す. また読み出すにはブロックを近づけ, 0になるまでの回数で知る.
A, B, C, などが記憶場所で, その上方にブロックを置き, そのブロックまでの距離を記憶している値とする. 従って書き込むにはその数値の分だけブロックを遠ざける手続きを繰り返す. また読み出すにはブロックを近づけ, 0になるまでの回数で知る.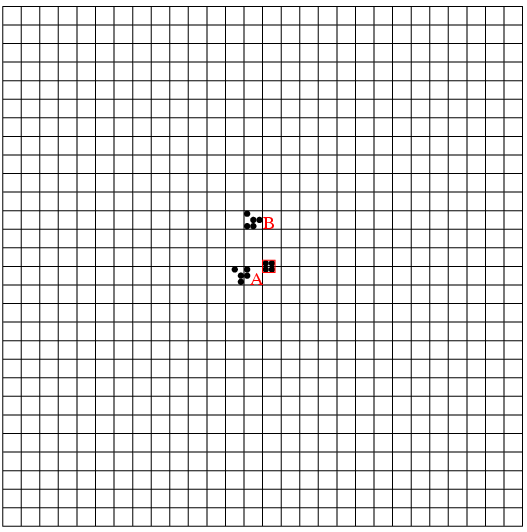
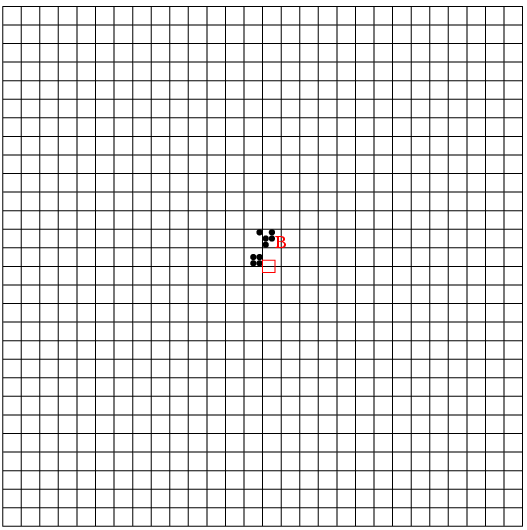
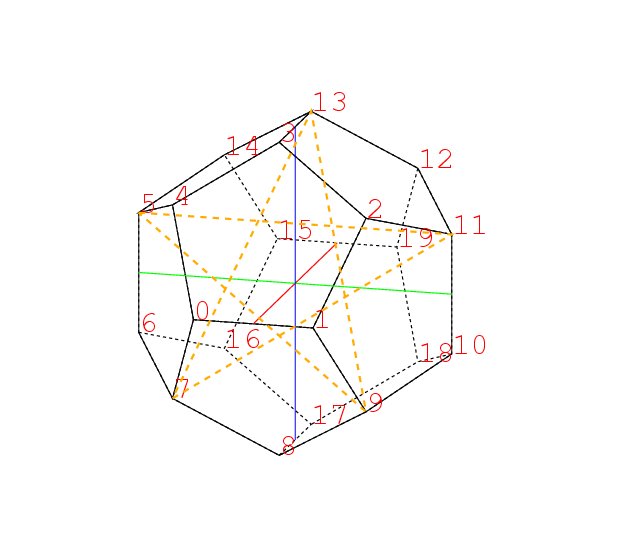
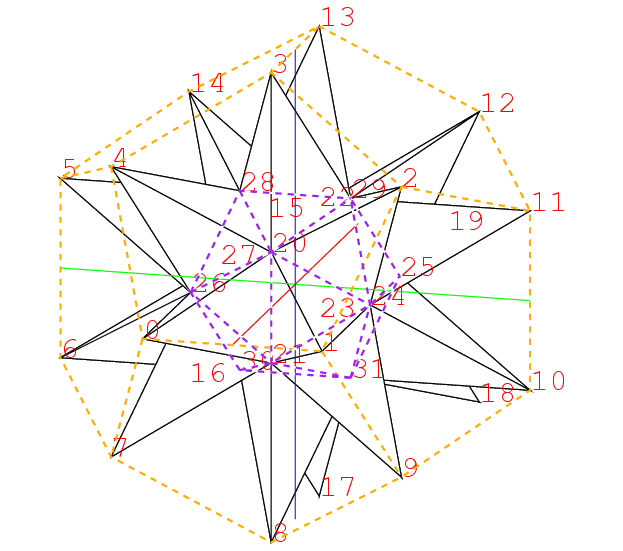
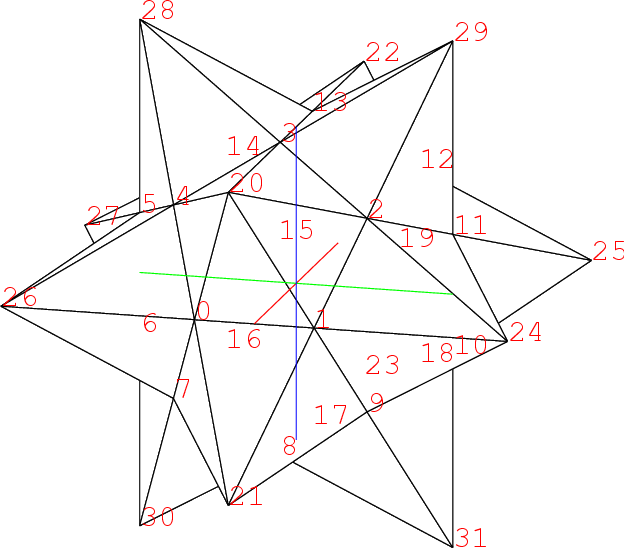
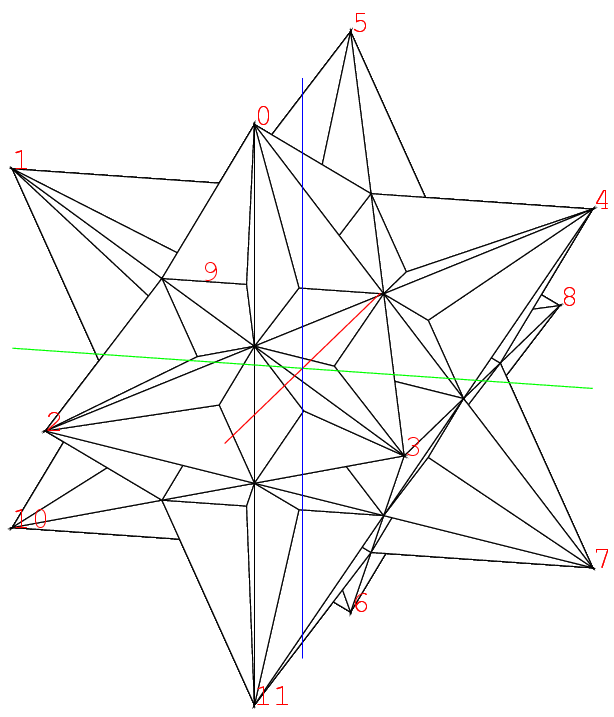
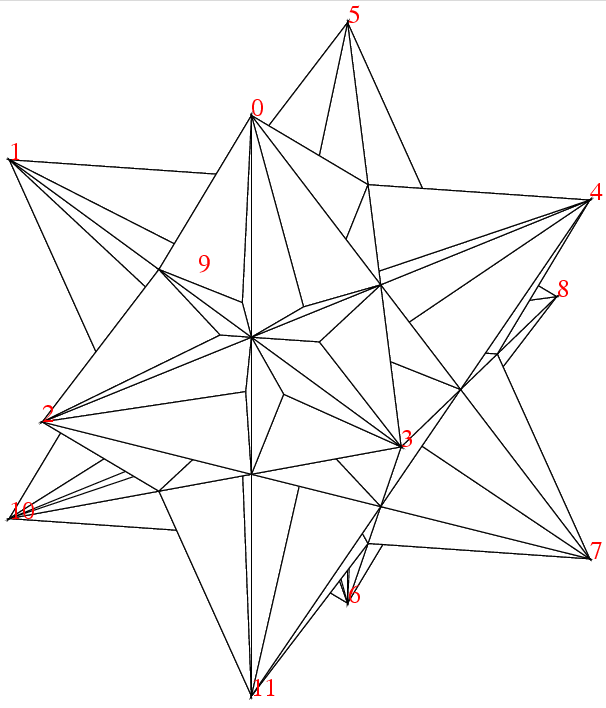
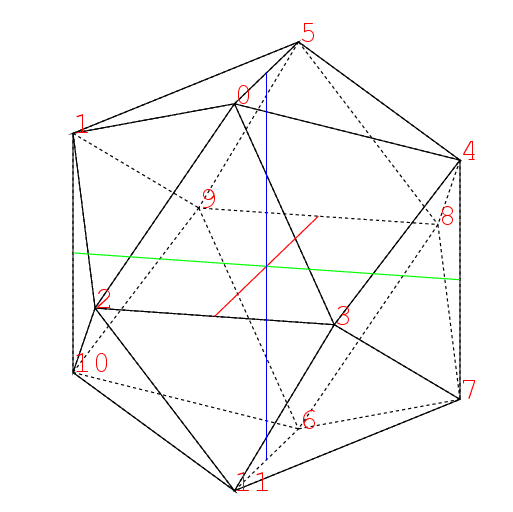 つまり頂点0,1,2の面に対しては, それに隣る三角形の頂点5,10,3の三角形で, こういう面だけで出来る立体はそう容易には想像出来ない. 数学者の想像力にはいつもながら脱帽だ. かなりの日時をかけ, 苦心惨憺, 紆余曲折, といいつつも十分楽しんだ末, 出来た図はこれだ. 自画自賛すれば実にもっともらしい.
つまり頂点0,1,2の面に対しては, それに隣る三角形の頂点5,10,3の三角形で, こういう面だけで出来る立体はそう容易には想像出来ない. 数学者の想像力にはいつもながら脱帽だ. かなりの日時をかけ, 苦心惨憺, 紆余曲折, といいつつも十分楽しんだ末, 出来た図はこれだ. 自画自賛すれば実にもっともらしい.
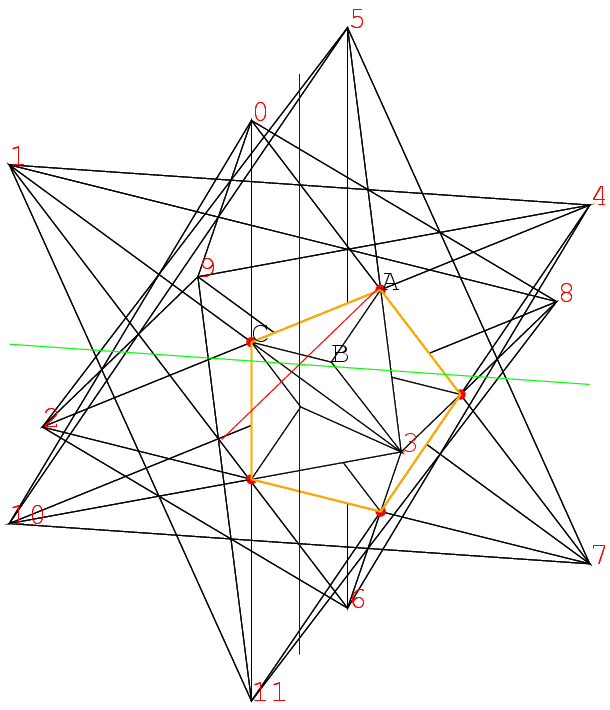 しかし頂点3に関わる部分だけで三角形は15もある. 都合180個の三角形の座標を計算しなければならぬ. 当然その計算の部分はSchemeで別にやることにした.
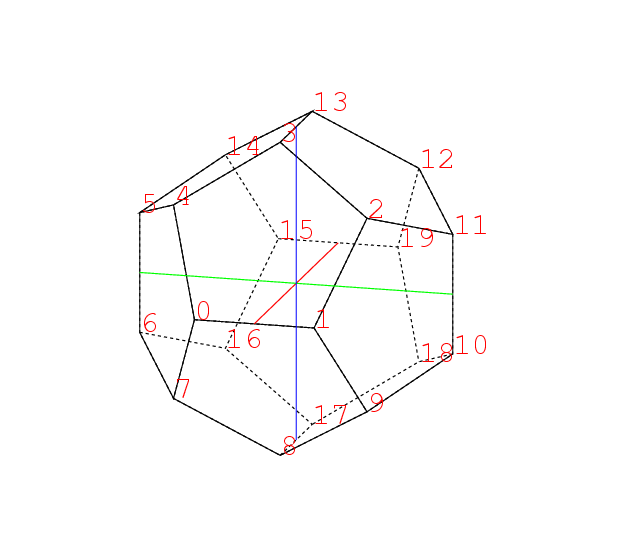
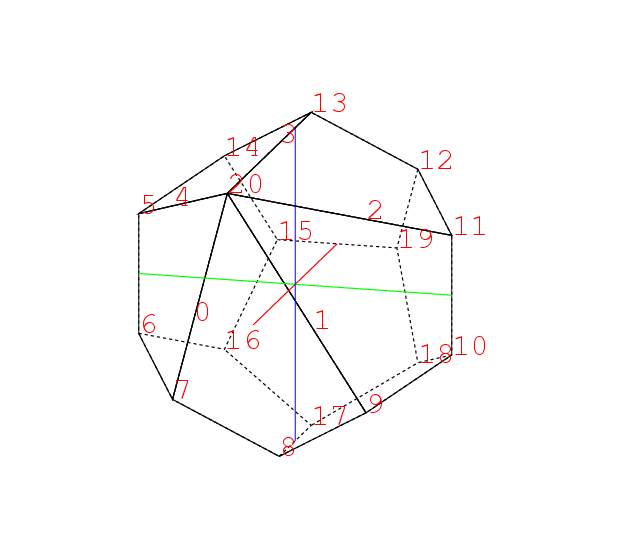
しかし頂点3に関わる部分だけで三角形は15もある. 都合180個の三角形の座標を計算しなければならぬ. 当然その計算の部分はSchemeで別にやることにした.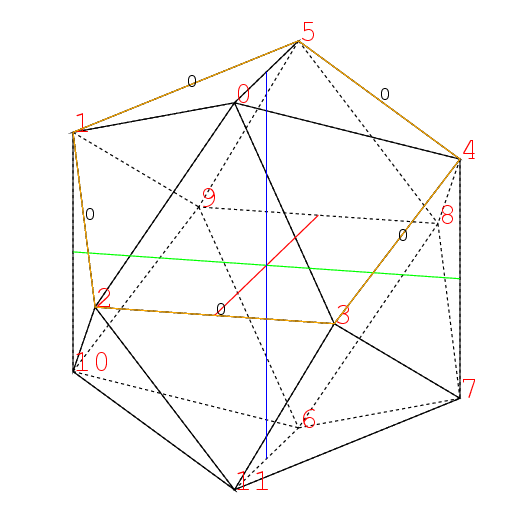 さらに頂点2と3に隣る頂点の面を作ると
さらに頂点2と3に隣る頂点の面を作ると
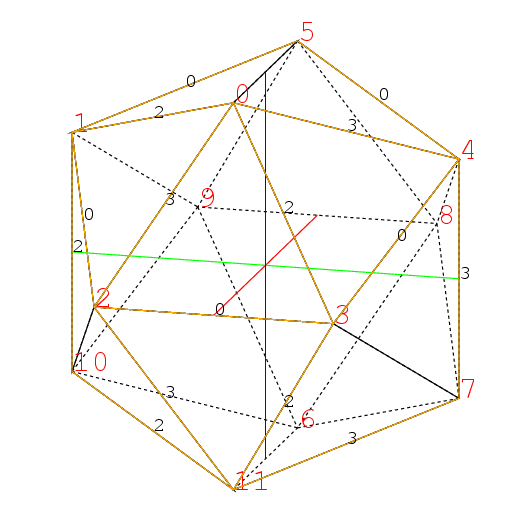 のように2に隣る面0,1,10,11,3と, 3に隣る面0,2,11,7,4が得られる,
ところで0に隣る面と2に隣る面は1と3で交わるからその交線は1から3へ引いた線である. 同様に0に隣る面と3に隣る面は2と4で交わるからその交線は2から4へ引いた線である. さらに2に隣る面と3に隣る面の交線は0から11へ至る.
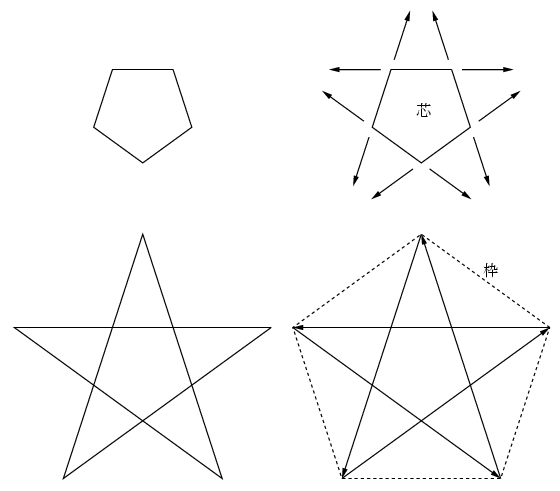
従ってもとの正二十面体の面の1つの三角形0,2,3の中に3つの交線が現れる. その交点を下の図のようにPとする.
のように2に隣る面0,1,10,11,3と, 3に隣る面0,2,11,7,4が得られる,
ところで0に隣る面と2に隣る面は1と3で交わるからその交線は1から3へ引いた線である. 同様に0に隣る面と3に隣る面は2と4で交わるからその交線は2から4へ引いた線である. さらに2に隣る面と3に隣る面の交線は0から11へ至る.
従ってもとの正二十面体の面の1つの三角形0,2,3の中に3つの交線が現れる. その交点を下の図のようにPとする.
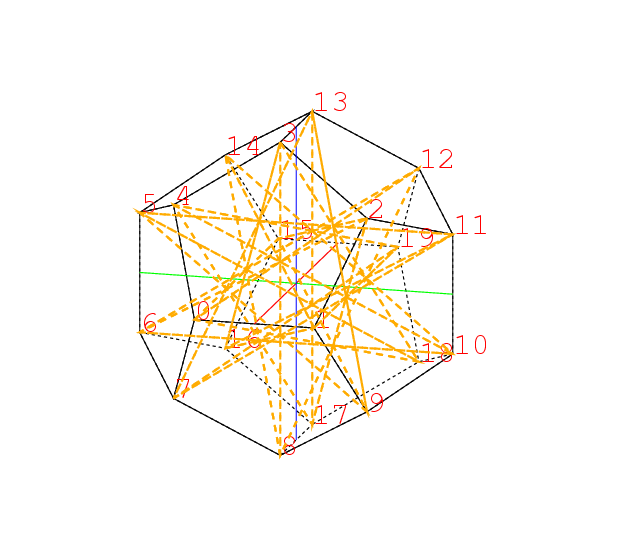
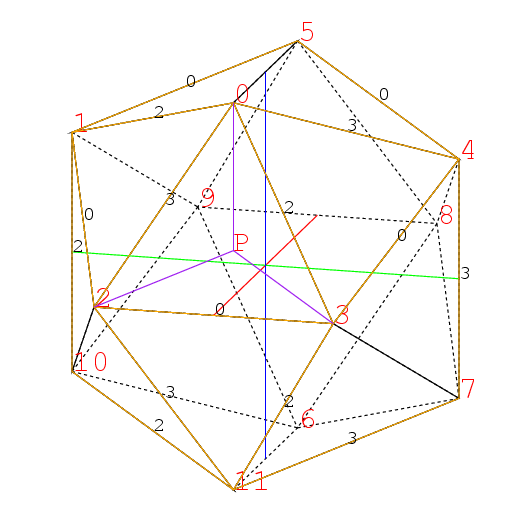 同様に三角形0,3,4の中に3つの交線が現れる. その交点を下の図のようにQとする.
同様に三角形0,3,4の中に3つの交線が現れる. その交点を下の図のようにQとする.
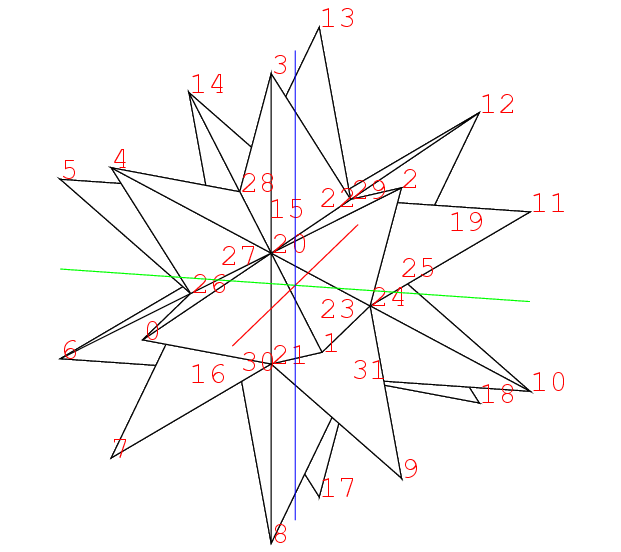
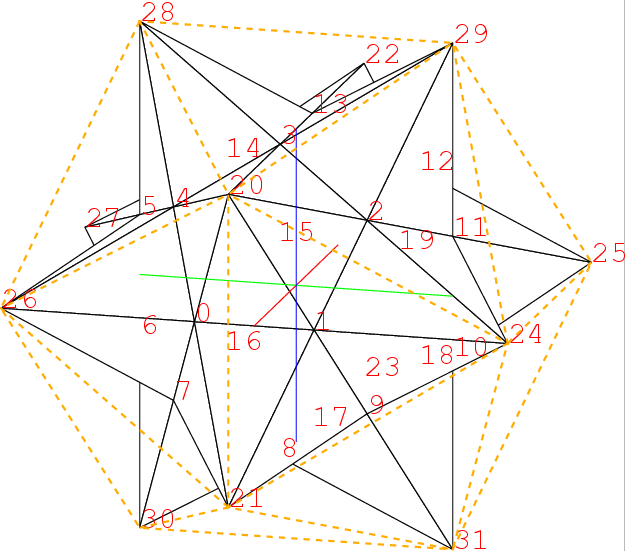
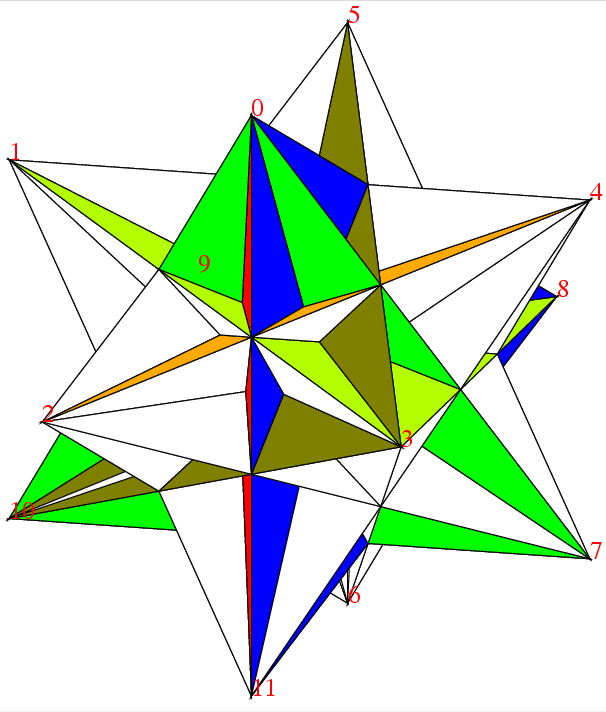
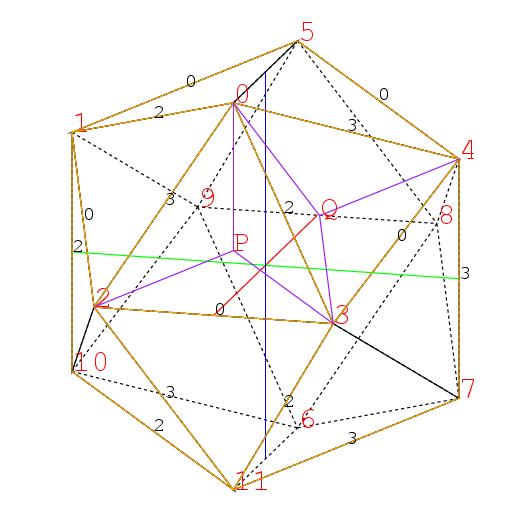 この2点の座標が決まると, 大十二面体を描くことが出来る. それがこれだ. この正多面体はPやQの所が凹んでいて, 水が溜まる形である. 右下の頂点3を中心とした昔の陸軍の徽章のような星形がみられる. 3の星の1つの枝は0の星の枝でもあるから, この枝は2等辺三角形である.
この2点の座標が決まると, 大十二面体を描くことが出来る. それがこれだ. この正多面体はPやQの所が凹んでいて, 水が溜まる形である. 右下の頂点3を中心とした昔の陸軍の徽章のような星形がみられる. 3の星の1つの枝は0の星の枝でもあるから, この枝は2等辺三角形である.
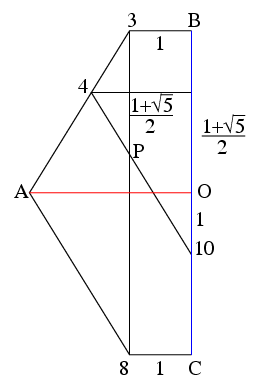
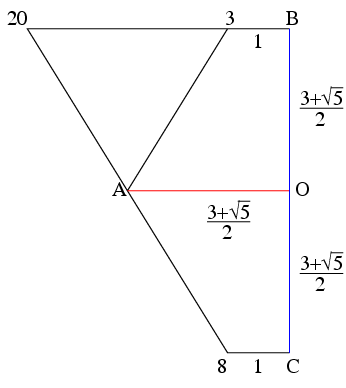
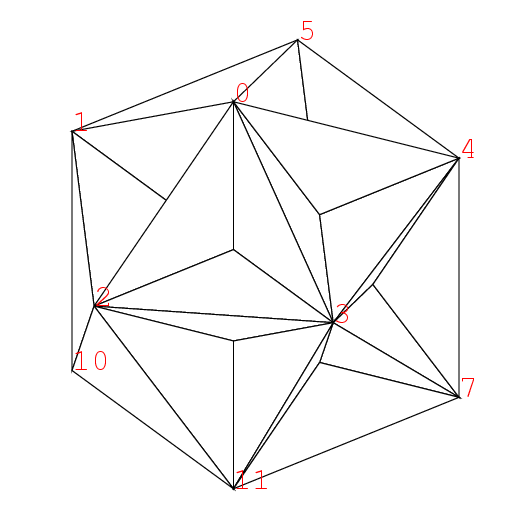 ところでPやQの座標の計算法だが, 正二十面体をx軸方向から見た図を描くと
ところでPやQの座標の計算法だが, 正二十面体をx軸方向から見た図を描くと
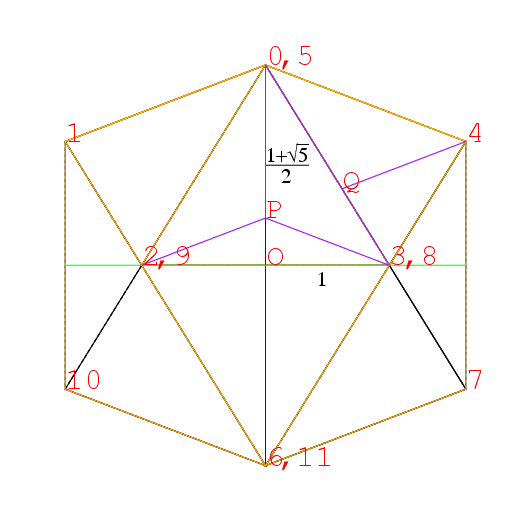 になる. この図で1, 10短い方の辺の長さを2とすると, 図の
0, 6の長さは1+√5. Oから0までは(1+√5)/2.
0, 3も1なので, これらからP, Qのz座標(3+√5)/2, (√5-1)/2が得られる.
これらを解くには (a+b√5)×(c+d√5)のような計算が頻発するから, この積がe+f√5であるとして, a,b,c,dからeとfを求めるプログラム
になる. この図で1, 10短い方の辺の長さを2とすると, 図の
0, 6の長さは1+√5. Oから0までは(1+√5)/2.
0, 3も1なので, これらからP, Qのz座標(3+√5)/2, (√5-1)/2が得られる.
これらを解くには (a+b√5)×(c+d√5)のような計算が頻発するから, この積がe+f√5であるとして, a,b,c,dからeとfを求めるプログラム