さて, そういう部品の一つに希薄銃(thin gun)というのがある. Life Gameで作る計算機の情報(信号)は, 2次元世界を飛び回わるグライダーだが, グライダー銃は30クロックごとにグライダー1個を発射し, これでは濃すぎる(多すぎる)ので, もっと間引いたグライダー列を作りたい. その機構が希薄銃である. 本当に出来るかなと思いやってみた.
次の図が希薄銃の様子を示す. これはProcessingのシミュレータで動いているもののある時点でのスナップショット(をPostScriptで書き直したもの)である.
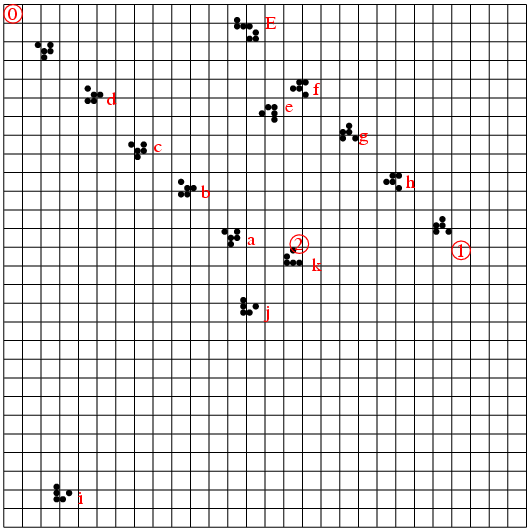
赤い丸で数字を囲ったのが3個所あり, それぞれグライダー銃がグライダーを発射する場所だ. 左上のグライダー銃0は, 右下へグライダーを出し続ける. 図に見えるグライダーに先頭からa, b, c,...と標識を付ける.
(グライダー銃はもっと複雑な形だが, こんな大きなものをシミュレータに書き込むと, 広い面積が必要になるので, このシミュレーションでは, シミュレータがどのタイミングにどの位置でどの方向へグライダーを発射するかのシナリオに従ってグライダーを発生する.)
右端の中ほどに1番のグライダー銃があり, これは左上へグライダーを送る. こちらのグライダーをf, g, h,...とする.
これらグライダーの2列の間で, eというグライダーが右上に向っている. これはConwayのいうキックバックで, eは2つのグライダー列の間を右上と左下で往復する. eは間もなくfと接触し, eとfは消滅し, eと逆向きのグライダーが出現する.
そうして戻ってくるキックバックのグライダーは, タイミング的には0番のグライダー列のdと接触し, dを消し, また右上へキックバックする.
eが前回右上に向う前に, 左下へ向っていたグライダーはaの1機前のグライダーに衝突し, 右上へキックバックしていたのである. 0番のグライダー列は, したがって, a, b, cとキックバック地点を通過した後, dは消滅し, その後また3個通過し, 1個消滅する,... を繰り返す.
左上へ進んでいる1番のグライダー列も, 4個に1個はキックバックで消えるが, 3個はキックバックされずに通過する. しかしキックバック後のグライダーは要らないから, Eと書いたイーターで吸い込む.
上の図には中央あたりに2番のグライダー銃があり, グライダーを左下へ発射している. そこへキックバックを回避してきた0番のグライダー列が近づく. この衝突は, 両者が消滅する位相であって右下へ通過するグライダーはないが, すでにキックバックで消えた0番グライダーに対応するホールでは, 2番のグライダーは衝突を免れ, 左下へ進む. 図の左下のグライダーiは, そのように抜けてきたものである. その後3機の2番のグライダーは, キックバックを免れた0番のグライダーのために消滅してホールになる. jはaの前のグライダーがホールだったため, 抜けてきたのである.
このようにして, キックバックで3/4になった0番のグライダー列により, 1/4に希薄になったグライダー列が発生出来る.
次は, キックバックの起こし方だ. グライダーの位置決めのため, ある方向に進むグライダーの4位相パターンのそれぞれに, 注目点を決めよう.
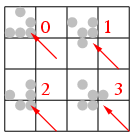
この右下へ移動するグライダーの図で, 左上, 右上, 左下, 右下が赤字のようにそれぞれ位相0,1,2,3で, 一番進行方向に近い場所を注目点とする. 位相0はいわゆるハッカーエンブレムの形で, 4クロック後には右へも下へも1セル分移動する.
Conwayの示すキックバック機構の図は以下の通り.
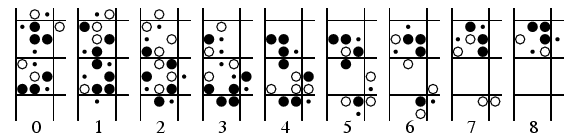
白黒を問わず, 丸が生きているセルである. 下の数字0から8は相対クロックだ. クロック0では上に左下へ進むグライダー, 下に右下へ進むグライダーが見える. 黒丸は次のクロックでも生き残るセル. 白丸は次には消えるセル, 点は今は死んでいるが, 次のクロックで生まれるセルだ.
この反応を経て, クロック6,7,8では右上へキックバックされるグライダーが形成され, 8が丁度0と180度逆転している. つまり, ターンで8クロックかかるわけだ.
グライダーの列は30クロック間隔なので, 向こうでもう一度キックバックされ, 30の倍数で戻ってくれば, 後続のグライダーとうまく衝突出来る. こちらのターンで8, 向こうで8かかると, 16クロック. 1歩進むのに4クロックかかるから, その距離往路と復路で8クロック. 16足す何倍かの8クロックの和で30の倍数になるのは,
30=16+8*1.75
60=16+8*5.5
90=16+8*9.25
120=16+8*13
だから, 最後のが解で13ステップの距離を往復し, 片側で120クロック毎にキックバックを起すことになる. 120はグライダー間隔30クロックも4倍なので, 4機に1機が犠牲になる.
この計算から分かるように, 240クロックでもグライダー間隔を28にすればキックバック出来る. Conwayの記述には, 1/Nに希釈出来るが, Nは4の倍数でなければならないとある.
先ほどの図で, グライダー0とキックバックしたとして, 次のグライダー1とのキックバックはどこだろうか. タイミング0の下のグライダーの注目点(下の3x3の正方形の右下)をx=0,y=0とすると, タイミング8の右上に出発しようとするグライダーの注目点はx=0,y=5である(yは上向きに測る.)
次の衝突のタイミング0は13セル間隔離れているから, x=13, y=18, つまりタイミング0の上のグライダーの注目点がそこである. 従って, その時点で1番のグライダーの注目点は, 0の下のグライダーと180度回転した形で, xが1少なく、yが4多い. x=12, y=22にグライダーがあれば良い. そのタイミングでグライダーを発射するように1番のグライダー銃を配置する. または, xとyを1ずつ遠ざけると, 発射の位相を4早める.
キックバックの図を描くプログラムを利用して, 2個のグライダー消滅の様子も描いてみよう.
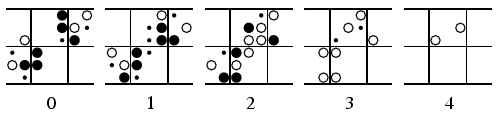
この図のように, 左上から来るグライダー(下)と右上から来るの(上)とが, この位置で出会うと4クロック後に消滅する. 右上の2番から出続けるグライダーは, 左上のグライダーがあると消滅し, ないと飛び続けるから, これをNot回路という.
シミュレータを使うノウハウも結構たまったので, またいろいろ遊べそうだ.

0 件のコメント:
コメントを投稿