ハノイの塔の円板の動かし方は誰でも知っているが, 任意の回数の手順の後, 各円板のある杭を示すアルゴリズムについてである.
円板4枚でまずやってみる. +-+-+線の上は3本の杭に円板が乗っている様子で円板を8,4,2,1とする.
1 2 2 1 1 4 4 4 4 1 1 1 1 2 2 2 8 8 1 8 1 2 8 2 8 4 2 8 4 2 8 4 8 4 4 8 +-+-+ +-+-+ +-+-+ +-+-+ +-+-+ +-+-+ +-+-+ +-+-+ +-+-+ 0000 0001 0021 0022 0122 0120 0110 0111 2111 1 2 2 2 1 1 1 1 4 4 4 4 4 8 2 4 8 2 4 8 2 8 2 1 8 1 8 8 +-+-+ +-+-+ +-+-+ +-+-+ +-+-+ +-+-+ +-+-+ 2112 2102 2100 2200 2201 2221 2222
+の杭を左から0,1,2とし, 各円板がどの杭にいるかを線の下に書いた. 当然円板8421の順だ.
さて, Winning Waysによるとn回目の後の様子は, nを二進法に展開し, 1,2,4,8,...の各ビットが1ならそれぞれ, 1, 21, 122, 2111に置き換え, 各桁を3を法として足す.
7回目で計算すると7=(111)2だから
0001 0021 0122 ---- 0111
となって円板8が杭0, 残りは杭1にあることが分かる.
schemeでプログラムを書くと
(define (mod3+ . d) (modulo (apply + d) 3)) (define (foo l) (if (null? (car l)) '() (cons (apply mod3+ (map car l)) (foo (map cdr l))))) (define (han n) (let ((b (n2bs n 4))) (foo (map (lambda (w p) (if (= p 1) w '(0 0 0 0))) '((2 1 1 1) (0 1 2 2) (0 0 2 1) (0 0 0 1)) b))))
各移動後の様子の計算の結果が
((0 0 0 0) (0 0 0 1) (0 0 2 1) (0 0 2 2) (0 1 2 2) (0 1 2 0) (0 1 1 0) (0 1 1 1) (2 1 1 1) (2 1 1 2) (2 1 0 2) (2 1 0 0) (2 2 0 0) (2 2 0 1) (2 2 2 1) (2 2 2 2))
となり上のと一致する.
ではなぜこれでよいか.
円板の移動はよく知られているように,
1は1,3,5,...回目に0→1→2→0→1→2→...と動き, 2は2,6,10,...回目に逆回りに動く.
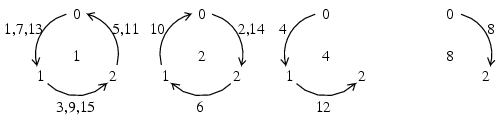
そこで各円板が各移動後にいる杭を書くことが出来る.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 0 1 1 2 2 0 0 1 1 2 2 0 0 1 1 2 2 0 0 2 2 2 2 1 1 1 1 0 0 0 0 2 2 4 0 0 0 0 1 1 1 1 1 1 1 1 2 2 2 2 8 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2
1回の時は二進表記は 0 0 0 1 なので, 上の1の列 0 0 0 1 を使う. 2回は 0 0 1 0 なので2の列 0 0 2 1 を使うことにする. 3回は1の列と2の列から3の列が得られるかと思うが, 単に足せば 0 0 2 2 となりよさそうだ. この伝でいろいろな列を3を法として足してみるといつもうまく行くことが分かる.
場当たり的なのがうまくいったので, 本質的なことを考えると, 8の円板が動く前と後との1から4までの円板の動きは, 前が 0 0 0 から 1 1 1 への移動, 後が 1 1 1 から 2 2 2 への移動だが, 移動のパターンは同じである. 最初 0 0 0 0 から8の移動直前の 0 1 1 1 までと, 8の移動後の 2 1 1 1 から最後の 2 2 2 2 までは, 結局 2 1 1 1 に 0 1 1 1 を足すに他ならない. それが4や2の円板でも同じなのだから当然なわけだ.

0 件のコメント:
コメントを投稿