軌跡作図器

學士會会報No.912 (2015-III)の表紙の図に興味をもった. 説明には独国マルチン・シリング(ハーレ社)製「軌跡作図器(Serie XXIV, Modell nr.11)」とあるが, それに続く説明は要領を得ないので改めて説明したい.

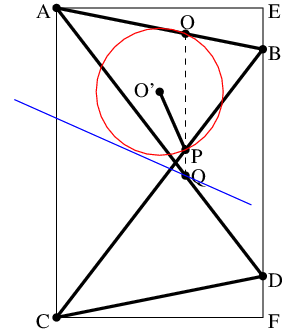
同じような図をネットで探して頂いてきたのが次の図だ.(http://goo.gl/Fpfcqt)



リンクABとCDの長さは等しく, ADとBCの長さも等しい. A,B,C,Dはピボットで連結されていて角度は変わる. AB, CB, ADのそれぞれをm : (1-m)に内分した点をO,P,Qとする(0 < m < 1).

Oは固定点で, ABはOを支点に回転する. PにPO'がOO'に等しくなるようなリンクPO'を取付け, O'も固定する. つまりPはO'を中心に円を描き, この円はOを通る.

こうしてPが円(の一部)を描くと, Qは直線の軌跡を描くという道具であった(Hartのinversorという名前である).

上の図を次のように書き直す. 太線がリンク機構である. 三角形ACBと三角形CADは逆向きだが合同だから, ACとBDは平行. ABDCは等脚台形になる. OPQは一直線でこれもACに平行.



BD上にA, CからACに垂線を立ててE,Fとする. EB=DFだから
AC×BDはEF×BD=(ED+EB)×(ED-EB)=ED²-EB².
ED²+AE²=AD²
EB²+AE²=AB²
だから
AC×BC=AD²-AB²
AO/AB=CP/CB=AQ/AD=mだから
OP=m×AC, OQ=(1-m)×BD
従って
OP×OQ=m×(1-m)×(AD²-AB²)=一定.

OP'×OQ'=OP×OQ=一定 でP'がOPの中点O'を中心とする円を動くと, Q'はQでOQに直交する線上を動く.



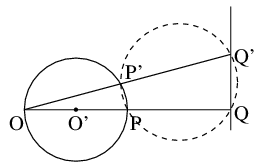
上の図で∠OP'P=∠R. ∠PQQ'=∠R だから4点PQQ'P'は円周上にあり, 方冪の定理(定点を過ぎる直線が定円と交わるとき, 定点より2つの交点までの長さの積は一定) によりOP'×OQ'=OP×OQ.

そのうちJavaScriptで動かしたいと思う.