SATソルバ

TAOCP 7.2.2.2は充足可能性(Satisfiability)が話題だ. 最初の方に多くの問題が CNF(Conjunctive Normal Form 乗法標準形)で記述できるという話が続く. 私はこの分野にはさほど興味がなく, まったくのど素人で, いつものようにアルゴリズ ムにだけ関心がある. 繰り返すまでもなく, TAOCPのアルゴリズムは自然言語で 記述されているから, その英文解釈が煩わしく, いつもああでもない, こうでもない と思いつつSchemeに変換し, いくつかの例題が無事に解けるのをみてやっと 安心している.

今回もそういう話である.

早速例をTAOCPから拝借すると, 乗法標準形は次のようなものである.


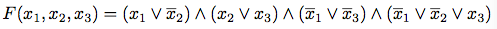
x₁, x₂, ...などが変数(variable). 変数または その上に線を引いたものがリテラル(literal). リテラルを∨でつないだものが 論理和節(clause), そしてCNFはそれらの節を∧でつないだものである.

かっこや∧や∨をいちいち書くのも面倒だということで, TAOCPではこれを


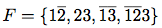
のように書いた.

さてSATソルバはFが真になるように, これらの変数に真(1), 偽(0)を対応させる もので, この例のサイズなら目の子で探せば解が見つかるが, 実用になる問題では 変数の個数がすごく多く, 高速なアルゴリズムが研究対象になっているらしい. ( 4月23日のブログMcGregorグラフを解く場合は440変数の1406論理和節になるとか.)

TAOCPにはまず基本的なアルゴリズムが出ていたので, 練習としてそれを Schemeで実装してみた.

まず上のCNFの例は, 私の実装ではS式で((1+ 2-) (2+ 3+) (1- 3-) (1- 2- 3+)) と書くことにする. 負のリテラルに-がつくだけでなく, 正のリテラルに+が つくのは対称性からきれいではないか. Schemeでは+1は数だが, 1+はシンボルになる. 従って 1+を1-にしたり, その逆にしたりは

(define (neg l)
(let* ((s (symbol->string l)) (w (- (string-length s) 1)))
 (string-set! s w (integer->char 
  (- 88 (char->integer (string-ref s w)))))
 (string->symbol s)))

つまりリテラルlを貰い, その文字列sとその長さ-1のwを 作る. 最後の+か-を取り出し, ASCIIの値とし,

(char->integer #\+) => 43
(char->integer #\-) => 45

だからその和の88から引くと+, -が逆転できる. ついでだが, 変数の記号からリテラルを作る(例えば x からx+, x-, 2 から2+, 2-を作る)手続きは次のようだ.

 (define (lit v s)
  (string->symbol (string-append
   ((if (number? v) number->string symbol->string) v)
   (symbol->string s))))
(lit 'x '+) => x+
(lit 'x '-) => x-
(lit 2 '+) => 2+
(lit 2 '-) => 2-

TAOCPにあるSATソルバの基本的なアルゴリズムB(F)(7222-56)は次のようだ.





考えてみると, このアルゴリズムは当然と思える. Fは節がandで繋がってい るから, 空のandは真だ. (and) => #t.

andで繋がっている節に空のものがあると, 空の節は(or) => #f だから Fは偽になる.

そのどちらでもないなら, まだFに残っている変数の正と偽のリテラル を作り, それで「ただし」以下のF|lを用意してBに 再帰的に作用させ, その結果にリテラルを足したのを返す.

「ただし」の内容はこうだ. lを含む節は真なので, andの並びでは 考慮する必要がないから削除する. 一方lの否定を含む節はorに 偽の項は関係ないから項を削除する. いずれにしろlの変数は 消えることになる.

そうだと思って書いたのが次のSchemeのプログラムである.

(define (b f vs)
 (define (lit v s)
  (string->symbol (string-append
   ((if (number? v) number->string symbol->string) v)
   (symbol->string s))))
 (let ((a '()))
  (define (b1 f ls vs)
   (display (list 'b1 f ls vs )) (newline)
   (cond ((member '() f) #f)
         ((= (length (nub f)) 1)
          (set! a (cons (cons (caar f) ls) a)))
         (else
         (let ((l (lit (car vs) '+)))
           (b1 (apb f l) (cons l ls) (cdr vs)))
         (let ((l (lit (car vs) '-)))
           (b1 (apb f l) (cons l ls) (cdr vs))))))
 (b1 f '() vs) a))

引数のvsは変数のリストである.

だから上の例では

(b '((1+ 2-) (2+ 3+) (1- 3-) (1- 2- 3+)) '(1 2 3))

と呼び出す. 内部手続きb1が途中経過を示すので, 出力は

(b1 ((2+ 3+) (3-) (2- 3+)) (1+) (2 3))
(b1 ((3-) (3+)) (2+ 1+) (3))
(b1 (()) (3+ 2+ 1+) ())
(b1 (()) (3- 2+ 1+) ())
(b1 ((3+) (3-)) (2- 1+) (3))
(b1 (()) (3+ 2- 1+) ())
(b1 (()) (3- 2- 1+) ())
(b1 ((2-) (2+ 3+)) (1-) (2 3))
(b1 (()) (2+ 1-) (3))
(b1 ((3+)) (2- 1-) (3))
=> ((3+ 2- 1-))

トレースの最初の行は, 後ろから見て残りの変数は2と3, リテラルは1+. 従って((1+ 2-) (2+ 3+) (1- 3-) (1- 2- 3+))の左端の項は1+があるから削除. 次は1+, 1-もないからそのまま, 次の2項は1-を削除. そして((2+ 3+) (3-) (2- 3+))を得る.

次の行はリテラルが2+. そこで(2+ 3+)は削除. (2- 3+)の 2-を削除. ((3-) (3+))が残る.

次. 変数3に対して3+, 3-をリテラルとしても()が得られ. εなので 充足不能になる. バックトラックして2-をリテラルにしても失敗.

改めて1-をリテラルにしてみたところ, fが空リストになり成功した.

原理的にはこれでよいが, 実用的には工夫があるらしい. そういう改良 アルゴリズムの話がTAOCPでは続く. その説明はまたいずれ.